AC自动机

听说不难学？

给定 n 个模式串和一个主串，查找有多少个模式串在主串中出现过

构造 trie 树，如果节点是模式串，cnt[u]++
构造自动机，即建边

回跳边指向父节点的回跳边所指向节点的儿子，例如：7 号点的回跳边是 3 号点

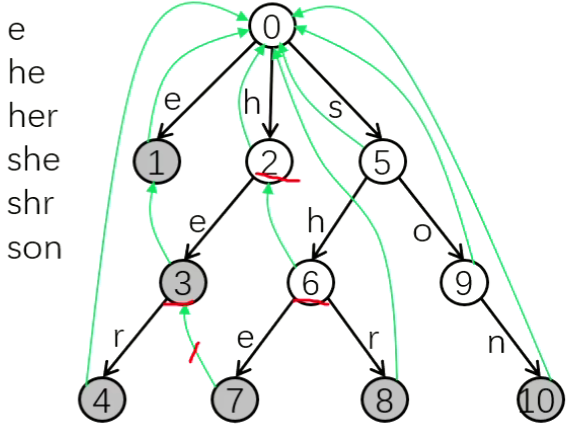
回跳边所指节点是当前节点的最长后缀，例如，7 号点是 she，最长后缀是 he

转移边指向当前节点的回跳边所指节点的儿子，例如 ch[7][r] 就是 4，意义是：转移边所指节点是当前节点的最短路（he）

bfs 建边：

若儿子存在，则父亲帮儿子建立回跳边
不存在，父亲自建转移边

查找：

i 指针沿着树边或者转移边走，不回退
j 指针沿着回跳边搜索，把当前节点的所有后缀模式串一网打尽

c++

void build() {
    queue<int> q;
    for (int i = 0; i < 26; i++) {
        if (tr[0][i]) {
            q.push(tr[0][i]);
        }
    }
    while (q.size()) {
        int u = q.front();
        q.pop();
        for (int i = 0; i < 26; i++) {
            if (tr[u][i]) {
                ne[tr[u][i]] = tr[ne[u]][i];
                q.push(tr[u][i]);
            } else {
                tr[u][i] = tr[ne[u]][i];
            }
        }
    }
}

int query(char *s) {
    int u = 0, res = 0;
    for (int i = 1; s[i]; i++) {
        u = tr[u][s[i] - 'a'];
        for (int j = u; j && cnt[j] != -1; j = ne[j]) {
            res += cnt[j];
            cnt[j] = -1; // 这里是统计出现过，所以匹配到了就清空
        }
    }
    return res;
}

基本代码是上面的，当然存在很多变式和优化

看下面的图，发现沿着 fail 边跳了很多次，如果一步到位找到儿子有 c 的节点就好了，不如直接把 c 那个节点作为自己的儿子

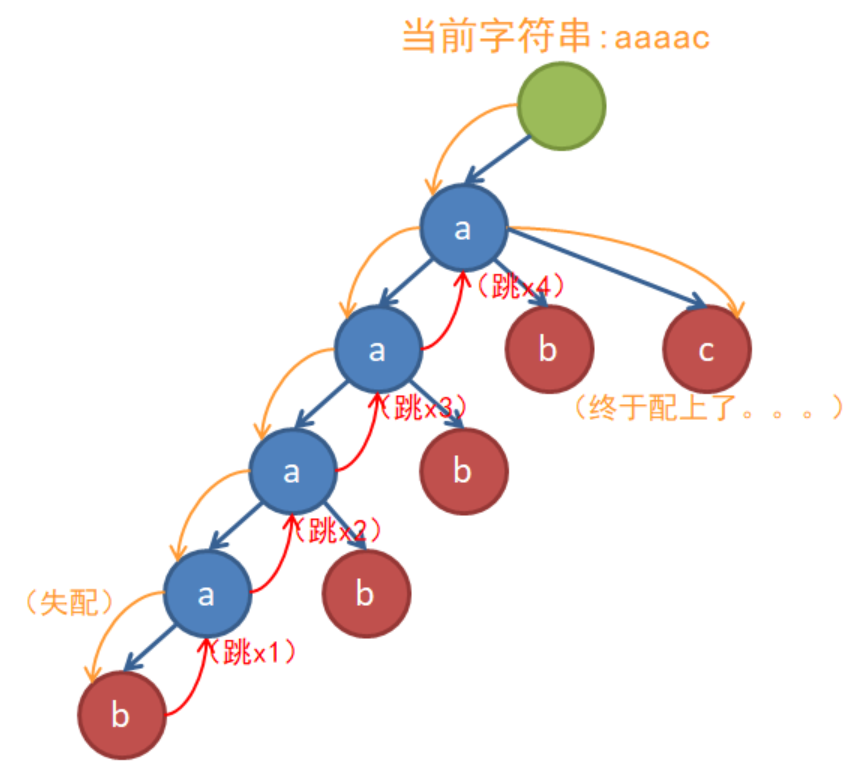
然后，加入一个 lst 数组，表示在它顶上的fail边所指向的一串节点中，第一个真正的结束节点，就可以跳过中间那些不是字符串结束位置的点了，每次计数时改为跳 lst 边

代码示例如下：100350. 最小代价构造字符串

c++

const int N = 5e4 + 10;
const int inf = 0x3f3f3f3f;
int sz, ch[N][26], val[N], f[N], lst[N], dep[N];
int dp[N];
void getfail(){
    queue<int> Q;
    f[0] = 0;
    for(int i=0; i<26; ++i){
        int u = ch[0][i];
        if(u){
            f[u] = 0;
            lst[u] = 0;
            Q.push(u);
        }
    }
    while(!Q.empty()){
        int r = Q.front(); Q.pop();
        for(int c=0; c<26; ++c){
            int u = ch[r][c];
            if(!u){
                ch[r][c] = ch[f[r]][c];
                continue;
            }
            Q.push(u);
            int v = f[r];
            while(v && !ch[v][c])   v = f[v];
            f[u] = ch[v][c];
            lst[u] = val[f[u]] == inf ? lst[f[u]] : f[u];
        }
    }
}
void update(int u, int i){
    if(u){
        dp[i] = min(dp[i], dp[i - dep[u]] + val[u]);
        update(lst[u], i);
    }
}
class Solution {
public:
    int minimumCost(string target, vector<string>& words, vector<int>& costs) {
        // 初始化及插入
        sz = 0;
        memset(ch[0], 0, sizeof(ch[0]));
        val[0] = 0;
        dep[0] = 0;
        for(int i=0; i<words.size(); ++i){
            string &s = words[i];
            int u = 0, c = 0;
            for(char v : s){
                c = v - 'a';
                if(!ch[u][c]){
                    ch[u][c] = ++sz;           
                    memset(ch[sz], 0, sizeof(ch[sz]));
                    val[sz] = inf;
                    dep[sz] = dep[u] + 1;
                }
                u = ch[u][c];
            }
            val[u] = min(val[u], costs[i]);
        }
        getfail();
        // 本题的 dp
        int len = target.length();
        dp[0] = 0;
        int u = 0, c = 0;
        for(int i=1; i<=len; ++i){
            dp[i] = inf;
            c = target[i-1] - 'a';
            u = ch[u][c];
            update(u, i);
        }
        if(dp[len] == inf)  return -1;
        return dp[len];
    }
};

灵神模板

c++

struct Node {
    Node* son[26]{};
    Node* fail; // 当 o.son[i] 不能匹配 target 中的某个字符时，o.fail.son[i] 即为下一个待匹配节点（等于 root 则表示没有匹配）
    Node* last; // 后缀链接（suffix link），用来快速跳到一定是某个 words[k] 的最后一个字母的节点（等于 root 则表示没有）
    int len; // 从根到 node 的字符串的长度，也是 node 在 trie 中的深度
    int cost = INT_MAX;
    
    Node(int len) : len(len) {}
};

struct AhoCorasick {
    Node* root = new Node(0);

    void put(string& s, int cost) {
        auto cur = root;
        for (char b : s) {
            b -= 'a';
            if (cur->son[b] == nullptr) {
                cur->son[b] = new Node(cur->len + 1);
            }
            cur = cur->son[b];
        }
        cur->cost = min(cur->cost, cost);
    }

    void build_fail() {
        root->fail = root->last = root;
        queue<Node*> q;
        for (auto& son : root->son) {
            if (son == nullptr) {
                son = root;
            } else {
                son->fail = son->last = root; // 第一层的失配指针，都指向根节点 ∅
                q.push(son);
            }
        }
        // BFS
        while (!q.empty()) {
            auto cur = q.front();
            q.pop();
            for (int i = 0; i < 26; i++) {
                auto& son = cur->son[i];
                if (son == nullptr) {
                    // 虚拟子节点 o.son[i]，和 o.fail.son[i] 是同一个
                    // 方便失配时直接跳到下一个可能匹配的位置（但不一定是某个 words[k] 的最后一个字母）
                    son = cur->fail->son[i];
                    continue;
                }
                son->fail = cur->fail->son[i]; // 计算失配位置
                // 沿着 last 往上走，可以直接跳到一定是某个 words[k] 的最后一个字母的节点（如果跳到 root 表示没有匹配）
                son->last = son->fail->len ? son->fail : son->fail->last;
                q.push(son);
            }
        }
    }
};

TsReaper 模板

cpp

// AC 自动机模板开始

const int MAXTOT = 1e5;

struct AhoCorasick {
    int tot, ch[MAXTOT + 10][26], dep[MAXTOT + 10], fail[MAXTOT + 10];

    int newNode(int d) {
        int ret = tot++;
        memset(ch[ret], 0, sizeof(ch[ret]));
        dep[ret] = d;
        fail[ret] = 0;
        return ret;
    }

    void reset() {
        tot = 0;
        newNode(0);
    }

    AhoCorasick() { reset(); }

    void insert(const char *s) {
        int now = 0;
        for (int i = 0; s[i]; s++) {
            int c = s[i] - 'a';
            if (ch[now][c] == 0) ch[now][c] = newNode(dep[now] + 1);
            now = ch[now][c];
        }
    }

    void buildFail(const char *s) {
        queue<int> q;
        for (int c = 0; c < 26; c++) if (ch[0][c] > 0) q.push(ch[0][c]);
        while (!q.empty()) {
            int sn = q.front(); q.pop();
            for (int c = 0; c < 26; c++) {
                int x = ch[sn][c], y = ch[fail[sn]][c];
                if (x > 0) {
                    fail[x] = y;
                    q.push(x);
                } else {
                    ch[sn][c] = y;
                }
            }
        }
    }
} ac;

// AC 自动机模板结束

class Solution {
public:
    int minValidStrings(vector<string>& words, string target) {
        // 用 words 里的字符串构建 AC 自动机
        ac.reset();
        for (int i = 0; i < words.size(); i++) ac.insert(words[i].c_str());
        ac.buildFail(target.c_str());

        int n = target.size();
        long long f[n + 1];
        f[0] = 0;
        // 将 target 输入 AC 自动机，now 是 target 的第 i 个字符匹配的节点
        for (int i = 1, now = 0; i <= n; i++) {
            int c = target[i - 1] - 'a';
            now = ac.ch[now][c];
            // AC 自动机上匹配失败，返回无解
            if (now == 0) return -1;
            // 最后一次加上的前缀长度，就是当前节点的深度
            f[i] = f[i - ac.dep[now]] + 1;
        }
        return f[n];
    }
};

fail 指针的含义是：i 的 fail 指向 j，表示根到 j 的串是根到 i 的串的后缀

AC自动机 ​

AC自动机