并查集模板

class UnionFind {
    vector<int> fa; // 代表元

public:
    int cc; // 连通块个数

    UnionFind(int n) : fa(n), cc(n) {
        // 一开始有 n 个集合 {0}, {1}, ..., {n-1}
        // 集合 i 的代表元是自己
        ranges::iota(fa, 0);
    }

    // 返回 x 所在集合的代表元
    // 同时做路径压缩，也就是把 x 所在集合中的所有元素的 fa 都改成代表元
    int find(int x) {
        // 如果 fa[x] == x，则表示 x 是代表元
        if (fa[x] != x) {
            fa[x] = find(fa[x]); // fa 改成代表元
        }
        return fa[x];
    }

    // 把 from 所在集合合并到 to 所在集合中
    // 返回是否合并成功
    bool merge(int from, int to) {
        int x = find(from), y = find(to);
        if (x == y) { // from 和 to 在同一个集合，不做合并
            return false;
        }
        fa[x] = y; // 合并集合。修改后就可以认为 from 和 to 在同一个集合了
        cc--; // 成功合并，连通块个数减一
        return true;
    }
};

字符串中最多出现次数减去最少出现次数

求出 的所有子串中，出现次数最多的字符次数与出现次数最少的字符次数之差。题意可转化为最大子数组和：枚举字符 和 ， 中的 看成 ， 看成 ，求最大子数组和。但是这里要求 必须出现，而一般的最大子段和 DP 是无法保证这点的，因此

• 用变量 维护 和 的出现次数之差，初始值为
• 用另一个变量 维护包含了 的 和 的出现次数之差，初始为 ，因为还没有遇到

        auto calc = [&](char a, char b) {
            int diff = 0, diff_b = -n;
            int res = 0;
            for (char c: s) {
                if (c == a) {
                    diff ++;
                    diff_b ++;
                } else if (c == b) {
                    diff_b = -- diff;
                    diff = max(diff, 0);
                }
                res = max(res, diff_b);
            }
            return res;
        };

变形：要求子串长度至少为 ，且 出现奇数次， 出现偶数次。对于子串长度，用滑窗来维护，即枚举 的时候，维护 表示左端点最右能到哪里，那么 左侧的位置都能选，把这些位置的信息存在前缀数组中，取出最小值即可。对于出现次数的限制，只需要满足 和 奇偶性相反， 和 的奇偶性相同即可。原题在 LC3445

// f[i][c]：前 i 个字符中，字符 c 出现了几次
// 求出奇数频率的字符为 x，偶数频率的字符为 y 的情况下的最大子数组和
auto gao = [&](int x, int y) {
    int ret = -INF;
    // g[0/1][0/1] 表示 x 和 y 在前缀里分别出现奇（偶）数次的最小前缀和
    int g[2][2];
    for (int i = 0; i < 2; i++) for (int j = 0; j < 2; j++) g[i][j] = INF;
    // 枚举子数组的右端点 i
    // j 是一个单调指针，表示子数组的左端点最大可以到哪
    for (int i = 1, j = 0; i <= n; i++) {
        while (i - j >= K && f[i][x] != f[j][x] && f[i][y] != f[j][y]) {
            int &t = g[f[j][x] & 1][f[j][y] & 1];
            t = min(t, f[j][x] - f[j][y]);
            j++;
        }
        int now = f[i][x] - f[i][y];
        // x 要出现奇数次，所以在前缀里频率的奇偶性必须不同
        // y 要出现偶数次，所以在前缀里频率的奇偶性必须相同
        ret = max(ret, now - g[f[i][x] & 1 ^ 1][f[i][y] & 1]);
    }
    return ret;
};

反悔贪心一题

题源 这里：有 只骆驼，你需要把这 只骆驼按照某种顺序，排成一行。 如果第 只骆驼在前 个位置中，那么它的幸福值是 ，否则是 。

技巧一： 的骆驼放在 的骆驼的左边是更优的（可以用交换法证明）。因此可以把骆驼分组计算

技巧二： 我们可以先把所有 加起来，然后讨论 怎么选取

技巧三： 按照 从小到大排序

采取「捡到西瓜，丢掉芝麻」的反悔贪心策略：

先把 入堆（最小堆），如果入堆后发现堆的大小超过当前的 ，则弹出堆顶的「芝麻」

        for (int i = 0, k, l, r; i < n; i++) {
            cin >> k >> l >> r;
            if (l > r) {
                res += r;
                a[k].push_back(l - r);
            } else {
                res += l;
                b[n - k].push_back(r - l);
            }
        }
        auto f = [&](vector<vector<int>> &a) {
            priority_queue<int, vector<int>, greater<int>> q;
            for (int i = 0; i < a.size(); i++) {
                for (int x: a[i]) {
                    res += x;
                    q.push(x);
                    if (q.size() > i) {
                        res -= q.top();
                        q.pop();
                    }
                }
            }
        };
        f(a);
        f(b);

简化版见 luoguP2949，很简单，自己做出来了

翻转子树使得全部点权 0

题源 ARC148C

给一棵树，点权为 ，每次询问会让 个点变成 ，每次操作把一个点及其子树全反转，回答最小操作次数

这道题的特点在于， 范围都是 ，不能暴力做

如果 get 到了解法会觉得挺简单的，说白了就是

• 一个点是 ，需要对它和所有儿子都操作一次
• 但是这样会多算，如果发现一个 的父节点也是 时就要减去一次

因此可以总结出下面的写法，复杂度是 的

        while (q -- ) {
            cin >> m;
            unordered_set<int> s;
            LL res = 0;
            // 数据的点集中会有父节点后被标记的情况 要把点集先存下来
            while (m -- ) {
                cin >> x;
                s.insert(x);
            }
            for (auto &x: s) {
                res += son[x];
                if (s.count(p[x])) {
                    res --;
                } else {
                    res ++;
                }
            }
            cout << res << '\n';
        }

每次相邻两数 +1 或 -1，能否使数组变为 0

题源 ARC119C

给定数组 a，每次操作，你可以选择两个相邻的数字，把它们都加一，或者都减一。

对于 a 的一个连续子数组 b，如果可以通过执行任意多次操作，使 b 的所有元素为 0，则称 b 为好子数组。

输出 a 的好子数组的数量。

时，需要满足

时， 需要满足

时，需要把两边消掉，变成 ，转化为

时，变成 ，转化为

这样就发现了性质：合法数组的奇数位置的和等于偶数位置的和。如果把其中一种位置和变成负的，就转化为数组和为 ，经典的前缀和问题

        map<LL, int> mp;
        mp[0] = 1;
        LL s = 0, res = 0;
        for (int i = 0, x; i < n; i++) {
            cin >> x;
            s += x * (i % 2 ? 1 : -1);
            res += mp[s];
            mp[s] ++;
        }

单调栈 + 二次差分

题源 2735. 收集巧克力 的线性做法

题意延申为：对于 j ∈ [1,k]，求出数组的每一个长为 j 的窗口的最小值之和

朴素做法是 的，假如 j 给定，对于 a[i] 来说，有多少个窗口的最小值会是它 => 单调栈！

记录每个数左边、右边连续几个数是大于它的，然后讨论 j 跟 L[i]、R[i] 的关系（见题解）

进而发现窗口数量是关于 j 的常函数或一次函数，这就可以用差分来优化

记录 F[j] 为长度为 j 时的答案，枚举每个 a[i]，看能对哪些 F[j] 产生影响，最后因为是二次差分，所以计算两次前缀和就是答案

记录 2735 的线性做法

class Solution {
public:
    typedef long long LL;
    long long minCost(vector<int>& nums, int x) {
        int n = nums.size();
        // 找出 nums 中最小的元素，并用其为首元素构造一个新的数组
        int min_idx = min_element(nums.begin(), nums.end()) - nums.begin();
        vector<int> tmp;
        for (int i = 0; i < n; ++i) {
            tmp.push_back(nums[(min_idx + i) % n]);
        }
        nums = move(tmp);

        vector<int> L(n), R(n);
        L[0] = n - 1;
        // 循环来看，右侧 nums[0] 是更小的元素，但不一定是第一个更小的元素，需要用单调栈计算得到
        for (int i = 0; i < n; ++i) {
            R[i] = n - i - 1;
        }
        stack<int> s;
        s.push(0);
        for (int i = 1; i < n; ++i) {
            while (!s.empty() && nums[i] < nums[s.top()]) {
                R[s.top()] = i - s.top() - 1;
                s.pop();
            }
            L[i] = i - s.top() - 1;
            s.push(i);
        }

        vector<long long> F(n);
        // 辅助函数，一次差分，将 F[l..r] 都增加 d
        auto diff_once = [&](int l, int r, long long d) {
            if (l > r) {
                return;
            }
            if (l < n) {
                F[l] += d;
            }
            if (r + 1 < n) {
                F[r + 1] -= d;
            }
        };
        // 辅助函数，二次差分，将 F[l..r] 增加 ki + b，i 是下标
        auto diff_twice = [&](int l, int r, long long k, long long b) {
            if (l > r) {
                return;
            }
            diff_once(l, l, k * l + b);
            diff_once(l + 1, r, k);
            diff_once(r + 1, r + 1, -(k * r + b));
        };

        // 进行操作需要的成本
        diff_twice(0, n - 1, x, 0);

        for (int i = 0; i < n; ++i) {
            int minv = min(L[i], R[i]);
            int maxv = max(L[i], R[i]);
            // 第一种情况，窗口数量 k+1，总和 nums[i] * k + nums[i]
            diff_twice(0, minv, nums[i], nums[i]);
            // 第二种情况，窗口数量 minv+1，总和 0 * k + nums[i] * (minv + 1)
            diff_twice(minv + 1, maxv, 0, (LL)nums[i] * (minv + 1));
            // 第三种情况，窗口数量 L[i]+R[i]-k+1，总和 -nums[i] * k + nums[i] * (L[i] + R[i] + 1)
            diff_twice(maxv + 1, L[i] + R[i], -nums[i], (LL)nums[i] * (L[i] + R[i] + 1));
        }

        // 计算两次前缀和
        for (int i = 0; i < 2; ++i) {
            vector<long long> G(n);
            partial_sum(F.begin(), F.end(), G.begin());
            F = move(G);
        }

        return *min_element(F.begin(), F.end());
    }
};

多少个 N 位正整数，数位和为 M

不能带前导 0，数据范围都是

前置思路是枚举第一位，然后看后面，先假设每个数位可以取到无穷，共有 种选法，然后考虑每个数位不能超过 9 的限制

常见思路是容斥，枚举 k，表示 k 个整数超过了 9，把这些数看成 10 + 任意，即看作总和减去 10k，方案数就是 ，超过的数的选择有 种，这里有容斥系数

根据容斥原理，满足第 i 个数超过 9 的性质为 ，目标是求出 的并集，这样的话套用容斥原理的定义就可以理解了

学习下代码，组合数、逆元代码见模板

LL get(int n, int k)
{
    if (n == 0) return k == 0 ? 1 : 0;
    LL res = comb(n + k - 1, n - 1);
    for (int i = 1; i <= n; i++)
    {
        LL t = comb(n + k - 1 - i * 10, n - 1) * comb(n, i) % mod;
        res = (res + (i & 1 ? mod - t : t)) % mod; // 系数是 (-1)^k
    }
    return res % mod;
}

    int n, m;
    cin >> n >> m;
    init();
    LL res = 0;
    for (int i = 1; i <= 9 && i <= m; i++)
    {
        int a = n - 1, b = m - i;
        res = (res + get(n - 1, m - i)) % mod;
    }
    cout << res << endl;

1-n 中，二进制位 1 有多少个？非 DP 做法

• 方法一：数学推导

（从右到左）首先考虑求最低位有几个 1，答案就是奇数个数，这很简单。第二位怎么办？先让 n 右移一位，然后再统计奇数可以吗？举个例子看看

001 -> 00
010 -> 01
011 -> 01
100 -> 10
101 -> 10
110 -> 11

会发现，01 是一个奇数，当我们统计一个 01 时，实际上对应了原来的两个数。例外情况：11 只对应了一个数。因此可以分两部分去统计：

1. n 左移 i 位后，每个奇数对应原来的 2^i 个数
2. 最后的那个奇数，对应的数不足 2^i，单独计算

这里怎么排除最后的奇数呢？做法是只统计到 1 ~ n/2 - 1

怎么单独计算？也是有些巧妙的，比如说

100
101
110
111

看最后两位 00 01 10 11，正好就是表示有几个数，因此可以用一个 mask 去得到

def count(num: int, x: int):
    res = 0
    shift = 0 # shift = x - 1
    n = num # n = num >> shift
    while n:
        # part 1
        res += (n // 2) << shift
        # part 2
        if n % 2:
            mask = (1 << shift) - 1
            res += (n & mask) + 1
        shift += 1 # shift += x
        n >>= 1 # n >>= x
    return res

进阶版：只统计那些 mod x == 0 的二进制位，即 3007. 价值和小于等于 K 的最大数字

那我们初始的时候要把 num 右移 x-1 位，然后再开始统计，每次循环都右移 x 位即可

• 3007. 价值和小于等于 K 的最大数字 的方法二：逐位构造

从高到低遍历每个位，要是这个位能填 1 就填 1，这样构造出的数字一定是最大的

设枚举到第 i 位时，i 左边有 pre 个符合题意的填了 1 的比特位

此时填 1 的话就新增了 2^i 个数

对 i 的左边，贡献 pre*2^i

对 i 的右边，有多少个符合题意，位为 1 的比特位？有 i/x 个。每个位可以贡献 2^(i-1) 个 1，因为固定这一位为 1，可以构造 2^(i-1) 个数

多少个连续区间连乘是 A 的倍数而非 B 的倍数

思路是通过质因数分解，用前缀和统计前 i 个数中，包含多少个 A 的第 j 个质因数（对 B 也是同理），然后枚举右端点，有多少个左端点呢？

利用双指针，假设对于右端点 i，左端点 p1 左边都满足连乘是 A 的倍数，一共有 p1 - 1 个数；左端点 p2 左边都满足连乘是 B 的倍数，一共有 p2 -1 个数，那么就有 max(0, p1-p2) 个符合题意的左端点，即意味着 p1 到 p2 为合法左端点

难点：双指针维护的是第一个不是倍数的位置

如何快速 check

    for (int i = 1; i <= n; i++) cin >> a[i];
    vector<PII> v1, v2;
    for (int i = 2; i * i <= A; i++)
    {
        if (A % i) continue;
        int cnt = 0;
        while (A % i == 0) A /= i, cnt ++;
        v1.push_back({i, cnt});
    }
    if (A > 1) v1.push_back({A, 1});
    for (int i = 2; i * i <= B; i++)
    {
        if (B % i) continue;
        int cnt = 0;
        while (B % i == 0) B /= i, cnt ++;
        v2.push_back({i, cnt});
    }
    if (B > 1) v2.push_back({B, 1});
    
    int m1 = v1.size(), m2 = v2.size();
    vector<vector<int>> pa(m1, vector<int>(n + 1));
    vector<vector<int>> pb(m2, vector<int>(n + 1));
    for (int i = 1; i <= n; i++)
    {
        for (int j = 0; j < v1.size(); j++)
        {
            int t = a[i], k = v1[j].x, cnt = 0;
            while (t % k == 0)
            {
                t /= k;
                cnt ++;
            }
            pa[j][i] = pa[j][i - 1] + cnt;
        }
        
        for (int j = 0; j < v2.size(); j++)
        {
            int t = a[i], k = v2[j].x, cnt = 0;
            while (t % k == 0)
            {
                t /= k;
                cnt ++;
            }
            pb[j][i] = pb[j][i - 1] + cnt;
        }
    }
    
    auto check1 = [&](int l, int r)
    {
        for (int i = 0; i < v1.size(); i++)
            if (pa[i][r] - pa[i][l - 1] < v1[i].y) 
                return false;
        return true;
    };
    
    auto check2 = [&](int l, int r)
    {
        for (int i = 0; i < v2.size(); i++)
            if (pb[i][r] - pb[i][l - 1] < v2[i].y) 
                return false;
        return true; 
    };
    
    for (int i = 1; i <= n; i++)
    {
        while (p1 <= i && check1(p1, i)) p1 ++;
        while (p2 <= i && check2(p2, i)) p2 ++;
        res += max(0, p1 - p2);
    }

逃跑——倍增法求期望

题意是给一棵树，A 在根节点，求出 B 在 i 号点时，每一秒 A B 各自移动（也可以不动），最多几秒后相遇，对于 i ∈ [1,n]，求出时间的期望值

首先看每个点怎么求，根据用例手玩可知

• B 向下移动到最远的叶子节点
• B 先往父节点移动，然后在某个父节点处，往下走到最远的叶子，这个过程不能与 A 相遇

倍增怎么运用？假设 B 的深度为 x，A 初始深度为 1，那么 B 有 x-1 个父节点，B 最多往上移动 (x-1-1)/2 个父节点，再多一个就会和 A 相遇了，这个父节点可以用倍增快速求得

用 dfs 维护每个点的子树中最远的叶子节点要走多少步，即 d[] 数组

void dfs(int u, int f)
{
    fa[u][0] = f, d[u] = 1, dep[u] = dep[f] + 1;
    for (int v: g[u])
        if (v != f)
        {
            dfs(v, u);
            d[u] = max(d[u], d[v] + 1);
        }
}

    for (int i = 1; (1 << i) <= n; i++) // lca
        for (int j = 1; j <= n; j++)
            fa[j][i] = fa[fa[j][i - 1]][i - 1];
    
    LL res = 0;
    for (int i = 2; i <= n; i++)
    {
        int t = (dep[i] - 1 - 1) / 2;
        int f = get(i, t); // i 的第 t 个父亲
        res = (res + dep[f] + d[f] - 2) % mod;
    }
    cout << res * qmi(n, mod - 2, mod) % mod << endl;

缺页异常 1

思路：

考虑一个用户，发出 m_i 条申请，枚举分配空间 [0,m_i]，计算出每个空间对应的缺页次数

怎么计算？由于替换算法会替换掉未来最久访问的，因此需要记录每个页面的下次访问时间，可以用哈希表记录。然后遍历每个请求，怎么找出需要替换的呢？技巧是用堆来做，配合一些懒删除的技巧（代码中使用了 set 来维护）

最后，已知第 i 个用户，分配 [0,m_i] 的代价，就可以使用 DP 来做：f[i][j] 表示前 i 个用户，一共分配 j 个页面的最小缺页次数。枚举第 i 个用户的分配空间即可，转移是很简单的

int work(int id, int sz)
{
    // 分配给 id 这个人 sz 个页面的缺页次数
    if (A[id].empty()) return 0;
    if (sz == 0) return A[id].size();
    
    unordered_map<int, int> mp;
    vector<int> nxt(A[id].size());
    for (int i = A[id].size() - 1; i >= 0; i--)
    {
        // 计算下次请求时间
        int &t = mp[A[id][i]];
        if (t > 0) nxt[i] = t;
        else nxt[i] = m + 1;
        t = i;
    }
    
    unordered_set<int> st; // 已经加入缓存的页面
    set<PII> pq; // 选出未来最久访问的页面
    int res = 0;
    for (int i = 0; i < A[id].size(); i++)
    {
        int x = A[id][i];
        if (st.count(x)) pq.erase({-i, x}); // 不再是最久访问页面
        else
        {
            res ++; // 缺页
            if (st.size() == sz) // 检查是否缓存满
            {
                PII p = *(pq.begin());
                pq.erase(pq.begin());
                st.erase(p.second);
            }
            st.insert(x);
        }
        pq.insert({-nxt[i], x});
    }
    return res;
}

void solve()
{
    cin >> n >> K >> m;
    for (int i = 1; i <= K; i++) A[i].clear();
    for (int i = 1; i <= m; i++)
    {
        cin >> x >> y;
        A[x].push_back(y);
    }
    for (int i = 1; i <= K; i++)
        for (int j = 0; j <= A[i].size(); j++)
            g[i][j] = work(i, j);
            
    // dp
    for (int i = 0; i <= K; i++)
        for (int j = 0; j <= n; j++) 
            f[i][j] = m + 1; 
    f[0][0] = 0;
    for (int i = 1; i <= K; i++)
        for (int j = 0; j <= n; j++)
            for (int k = 0; k <= A[i].size() && k <= j; k++)
                f[i][j] = min(f[i][j], f[i - 1][j - k] + g[i][k]);
    int res = m + 1;
    for (int j = 0; j <= n; j++) 
        res = min(res, f[K][j]);
    cout << res << endl;
}

缺页异常 2

思路：

假设有无限大的缓存，缓存的页从上到下最近访问时间递增，每次访问一个页，把它加到最上面；这里相当于只看无限缓存的前 k 个。因此，当出现一个页面请求时，如果页面从未出现，则所有大小的缓存都会缺页一次；否则，假设在第 t 个项，那么缓存大小为 [0,t-1] 的缓存都会缺页，这是一个前缀加，用差分数组维护

怎么知道当前请求页面在第几个项？一个页面被访问时，仍然在缓存中的条件是：该页面上次访问到这次访问间，不同的其它页面数不大于缓存大小。因此，需要处理出任意两个相同的数之间不同的数的个数即可。可以从左到右扫数组，每次将每种数字的最后一个设为 1，其它设为 0，区间求和即可，用树状数组维护

    for (int i = 1; i <= m; i++)
    {
        if (last[q[i]] == 0) res[m] ++; // 第一次出现
        else res[query(i - 1) - query(last[q[i]])] ++; // 查询不同数的个数
        
        update(i, 1);
        if (last[q[i]] != 0) update(last[q[i]], -1); // 上次出现位置置 0
        last[q[i]] = i;
    }
    for (int i = m - 1; i >= 0; i--) res[i] += res[i + 1];
    for (int i = 0; i <= m; i++) cout << res[i] << ' ';
    cout << endl;

多思路思考博弈题

Alice 和 Bob 轮流玩一个游戏，Alice 先手。 一堆石子里总共有 n 个石子，轮到某个玩家时，他可以 移出 一个石子并得到这个石子的价值。Alice 和 Bob 对石子价值有 不一样的的评判标准 。双方都知道对方的评判标准。 给你两个长度为 n 的整数数组 aliceValues 和 bobValues 。aliceValues[i] 和 bobValues[i] 分别表示 Alice 和 Bob 认为第 i 个石子的价值。 所有石子都被取完后，得分较高的人为胜者。如果两个玩家得分相同，那么为平局。两位玩家都会采用 最优策略 进行游戏。 请你推断游戏的结果

第一思路：猜，按照什么顺序排序？按 a[i] 还是 b[i] 还是 a[i]+b[i] 还是 a[i]-b[i]，验证样例后发现是 a[i]+b[i]

假设 Alice 的和为 A，Bob 的和为 B，前者需要最大化 A-B，后者需要最小化 A-B

第二思路：因为此题需要同时考虑 a 和 b，能不能只考虑一个？假设 Bob 先全部选了，然后 Alice 从中拿走一些；考虑拿走哪一个会使得 A-B 增量最大，发现增量就等于 a[i]-(-b[i])；进而转换为给定 sum 数组，Alice 每次拿走一个数，Bob 每次删除一个数，贪心思路就很明显了：按大到小操作

第三思路：拿两个石子 i, j 考虑，什么情况下 a[i]-b[j]>a[j]-b[i]？就自然转化为 a[i]+b[i] 的问题了，这种思路也叫做调整法

MST 典题

https://codeforces.com/problemset/problem/1245/D 已知一个平面上有 n 个城市，需要个 n 个城市均通上电。 一个城市有电，必须在这个城市有发电站或者和一个有电的城市用电缆相连。 在一个城市建造发电站的代价是 c[i]，将 i 和 j 两个城市用电缆相连的代价是 k[i]+k[j] 乘上两者的曼哈顿距离。 求最小代价的方案。

化点权为边权，建立虚拟源点，然后跑 MST，还要记录方案

代码中用 prim 实现

    LL tot = 0;
    vector<int> res;
    for (int i = 0; i < n; i++) {
        int t = -1;
        for (int j = 0; j < n; j++)
            if (!vis[j] && (t == -1 || c[j] < c[t])) t = j;
        vis[t] = 1;
        tot += c[t];
        if (p[t] == -1) res.push_back(t);
        for (int j = 0; j < n; j++)
            if (!vis[j]) {
                // 动态更新边权
                LL cost = 1LL * (k[t] + k[j]) * (abs(x[t] - x[j]) + abs(y[t] - y[j]));
                if (cost < c[j]) {
                    c[j] = cost;
                    p[j] = t;
                }
            }
    }
    cout << tot << endl;
    cout << res.size() << endl;
    for (int t: res) cout << t + 1 << ' ';
    cout << endl << n - res.size() << endl;
    for (int i = 0; i < n; i++)
        if (p[i] != -1) cout << i + 1 << ' ' << p[i] + 1 << endl;

0-1 MST

https://codeforces.com/problemset/problem/1242/B 有一张完全图，n 个节点 有 m 条边的边权为 1，其余的都为 0 问你这张图的最小生成树的权值

原题转换为求由 0-边构成的图的连通分量数-1

考虑 1-边最少的点 v，v 的 1-边数量 <= 2m/n（最小值不超过平均值）

拿这个 v 来构造连通分量，然后暴力遍历剩余的点构造，复杂度为 O(n+2m/n*n)=O(n+m)

    // 寻找 0-边最多的点 maxDeg0V
    int mxDeg0 = 0, mxV = 0;
    for (int i = 1; i <= n; i++) {
        int deg0 = n - 1 - g[i].size();
        if (deg0 > mxDeg0) mxDeg0 = deg0, mxV = i;
    }
    // 若图中没有 0-边，答案就是点的个数-1
    if (mxDeg0 == 0) {
        cout << n - 1 << endl;
        return 0;
    }
    
    vector<int> p(n + 1);
    for (int i = 1; i <= n; i++) p[i] = i;
    function<int(int)> find = [&](int x) {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    };
    // 将与点 v 以 0-边相连的点，合并到点 v 所属的连通分量上
    auto mergeEdge = [&](int v) {
        map<int, bool> vs;
        vs[v] = 1;
        for (int w: g[v]) vs[w] = 1;
        for (int i = 1; i <= n; i++)
            if (!vs[i]) p[find(i)] = find(v); // i-v 是 0-边
    };
    mergeEdge(mxV);
    for (int i = 1; i <= n; i++)
        if (find(i) != find(mxV)) mergeEdge(i); // 暴力遍历剩余的点
    // 计算联通分量个数-1
    int res = -1;
    for (int i = 1; i <= n; i++) res += (i == p[i]);
    cout << res << endl;

0-1 BFS

https://codeforces.com/problemset/problem/1063/B 在迷宫里走，限制是往左走不超过 x 步，往右走不超过 y 步，上下走无限制，问从起点出发，有多少空地格子可到达

题中有向左和向右两个约束，想办法减少约束：

从 (r,c) 走到 (x,y)，无论什么路径，向左走和向右走的步数差是相同的：l-r=c-y

因此最小化一个值即可，比如最小化 l，题意就转换成一个 0-1 bfs 问题

    q.push_back({r, c});
    dist[r][c] = 0;
    while (q.size()) {
        auto t = q.front();
        q.pop_front();
        for (int i = 0; i < 4; i++) { // i==1 表示向左
            int x = t.x + dx[i], y = t.y + dy[i];
            if (x < 0 || x >= n || y < 0 || y >= m || g[x][y] == '*') continue;
            if (dist[x][y] != -1 && dist[x][y] <= dist[t.x][t.y] + (i == 1)) continue;
            dist[x][y] = dist[t.x][t.y] + (i == 1);
            if (i == 1) q.push_back({x, y});
            else q.push_front({x, y});
        }
    }
    int res = 0;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < m; j++) {
            if (dist[i][j] == -1) continue;
            int a = dist[i][j], b = a - c + j;
            if (a <= X && b <= Y) res ++;
        }
    cout << res << endl;

折半搜索 + 二分查找

https://codeforces.com/problemset/problem/888/E 给一个数列和 m，在数列任选若干个数，使得他们的和对 m 取模后最大

数据范围是 35，先用 dfs 把前一半数的子集和都存下来，然后再 dfs 后半段，重点是，如何快速找出哪些方案可以匹配得出最大值？

由于存在取模，我们要分为当前方案 +s 大于等于 m 和小于 m 两种情况来讨论

• 当前 +s < m，可以转化为找一个最大的数满足 < m-s ，排序后二分即可
• 当前 +s >= m，取之前得到的最大值

最后需要特判 n=1 的情况

void dfs(int i, LL s) {
    if (i == n / 2) {
        tmp.push_back(s);
        return;
    }
    dfs(i + 1, s);
    dfs(i + 1, (s + a[i]) % m);
}

void dfs2(int i, LL s) {
    if (i == n) {
        int p = lower_bound(tmp.begin(), tmp.end(), m - s) - tmp.begin() - 1;
        //lower_bound找到第一个>=m-s的位置，从这个位置-1就是最大的符合<m-s的方案的位置
        res = max(res, tmp[p] + s);
        res = max(res, (s + tmp[tmp.size() - 1]) % m);
        return;
    }
    dfs2(i + 1, s);
    dfs2(i + 1, (s + a[i]) % m);
}

树中求路径点权 max-min 的转化

http://codeforces.com/problemset/problem/915/F 定义 f(i,j) 为树中 x 到 y 的路径的最大点权减去最小点权 对所有点对，求 f(i,j) 之和

经典贡献法，首先要想到拆成求 max 和求 min 两部分

两部分的处理方法是一样的，技巧是把点权转化为边权。求 max 时边权就是两个顶点的权值的 max，min 同理

然后是经典并查集处理技巧，把边排序（一个升序一个降序），然后边合并边统计答案，具体思路见茶 https://atcoder.jp/contests/abc214/tasks/abc214_d

struct Node {
    int x, y, w;
    bool operator<(const Node &t) const {
        return w < t.w;
    }
    bool operator>(const Node &t) const {
        return w > t.w;
    }
} a[N];

    for (int i = 1; i < n; i++) {
        cin >> a[i].x >> a[i].y;
        a[i].w = max(v[a[i].x], v[a[i].y]);
    }
    sort(a + 1, a + n);
    init(n);
    for (int i = 1; i < n; i++) {
        int x = find(a[i].x), y = find(a[i].y);
        if (x != y) {
            res += 1LL * sz[x] * sz[y] * a[i].w;
            p[x] = y;
            sz[y] += sz[x];
        }
    }
    for (int i = 1; i < n; i++) a[i].w = min(v[a[i].x], v[a[i].y]);
    sort(a + 1, a + n, greater<Node>());
    init(n);
    for (int i = 1; i < n; i++) {
        int x = find(a[i].x), y = find(a[i].y);
        if (x != y) {
            res -= 1LL * sz[x] * sz[y] * a[i].w;
            p[x] = y;
            sz[y] += sz[x];
        }
    }
    cout << res << endl;

每次询问回答以 u 为根的子树，出现次数不小于 k 的颜色种数

https://codeforces.com/problemset/problem/375/D 1e5 个点，颜色值，询问次数都是 1e5

离线查询 => 树上启发式合并

颜色出现次数 => 莫队思想

（统计子树信息 => dfs 序，不用这个也能做）

综合运用几种上述思想，用 c[u] 记录节点颜色，col[c[u]] 记录每种颜色出现次数，sum[col[c[u]]] 记录出现次数不小于的种数

void dfs(int u, int fa) {
    sz[u] = 1;
    L[u] = ++ tot;
    mp[tot] = u;
    for (int v: g[u])
        if (v != fa) {
            dfs(v, u);
            sz[u] += sz[v];
            if (sz[v] > sz[son[u]]) son[u] = v;
        }
    R[u] = tot;
}

vector<PII> que[N];
void add(int u) {
    col[c[u]] ++, sum[col[c[u]]] ++;
}
void sub(int u) {
    sum[col[c[u]]] --, col[c[u]] --;
}

void dfs1(int u, int fa, bool keep) {
    for (int v: g[u])
        if (v != fa && v != son[u]) dfs1(v, u, false);
    if (son[u]) dfs1(son[u], u, true);
    add(u);
    
    for (int v: g[u]) 
        if (v != fa && v != son[u])
            for (int j = L[v]; j <= R[v]; j++)
                add(mp[j]);
    
    for (auto &[idx, k]: que[u]) res[idx] = sum[k];
    
    if (!keep) 
        for (int j = L[u]; j <= R[u]; j++) sub(mp[j]);
}

不用 dfs 序的做法（更贴近模板）

void dfs(int u, int fa) {
    sz[u] = 1;
    for (int v: g[u])
        if (v != fa) {
            dfs(v, u);
            sz[u] += sz[v];
            if (sz[v] > sz[son[u]]) son[u] = v;
        }
}

vector<PII> que[N];

void count(int u, int fa, int x) {
    if (x == -1) sum[col[c[u]]] += x;
    col[c[u]] += x;
    if (x == 1) sum[col[c[u]]] += x;
    for (int v: g[u])
        if (v != fa && v != flag)
            count(v, u, x);
}

void dfs1(int u, int fa, bool keep) {
    for (int v: g[u])
        if (v != fa && v != son[u]) dfs1(v, u, false);
    if (son[u]) {
        dfs1(son[u], u, true);
        flag = son[u];
    }
    
    count(u, fa, 1);
    flag = 0;
    
    for (auto &[idx, k]: que[u]) res[idx] = sum[k];
    
    if (!keep) {
        count(u, fa, -1);
    }
}

寻找图中三角形

LCP 16. 游乐园的游览计划 对任意点 A，找两个经过 A 的三元环，使其覆盖的点权最大。点数 1e4，边数 1e4

以下笔记源自题解，记录下总结

• 暴力法：枚举边 (u,v)，用哈希表记录 u 的邻点，然后遍历 v 的邻点，看是否被记录

• 改进法：无向图定边：度数小的指向度数大的，相等则编号小的指向大的

  • 可以找出所有不重复的三元环，证明是只有 AB 才能找到，故只会找到一次
  • 复杂度降为 O(Msqrt(M))，证明考虑原度数超过 sqrt(M) 的点的数量

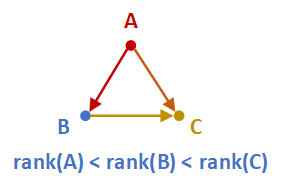
难点二：怎么找覆盖权值最大的两个三角形

枚举顶点，按照权值和大到小排序，权值和前三大的边中一定有一条包含在最优解中，证明思路可以通过枚举权值前三大的边的组合，分类讨论得到（要学会这个思维！）

难点三：代码怎么写

• 下面的代码实现了：把 AB 边放到 node[C] 中，把 BC 边放到 node[A] 中，以此类推，学会这个套路！

• 先把边排序，就自然得到了每个顶点对应的三元环中另外两条点的按权值和降序的结果！

• 枚举答案的时候，先定下权值和最大的边 a，然后枚举所有其他边

  • 优化一：枚举到一条边 k，顶点不相交时，可以 break 了，后面不会更优
  • 后续 a++ 后，枚举到 k-1 就行，因为 a+k>(a+1)+k
  • 上面优化很难想，不写也是可以的

class Solution {
public:
    int maxWeight(vector<vector<int>>& E, vector<int>& W) {
        int N = W.size(), M = E.size(), cnts[N];
       
        // 对边按权值和排序，以便之后对每个点，直接获得按权值和排序的边
        sort(E.begin(), E.end(), [&](vector<int>& a, vector<int>& b) {
            return W[a[0]] + W[a[1]] > W[b[0]] + W[b[1]];
        });

        // 统计各个点的度数（出边数量）
        memset(cnts, 0, sizeof(cnts));
        for(auto v : E) 
            ++cnts[v[0]], ++cnts[v[1]];

        // 将无向图重建为有向图
        vector<pair<int,int>> G[N];
        for(int i = 0; i < M; ++i) {
            if(cnts[E[i][0]] < cnts[E[i][1]] || (cnts[E[i][0]] == cnts[E[i][1]] && E[i][0] < E[i][1]))
                G[E[i][0]].push_back({E[i][1], i});
            else
                G[E[i][1]].push_back({E[i][0], i});
        }

        // 求所有的三元环，并按边归类
        vector<int> nodes[M];
        int vis[N], idxs[N];
        memset(vis, 0xff, sizeof(vis));
        for(int i = 0; i < M; ++i) {
            for(pair<int, int> &ne : G[E[i][0]])
                vis[ne.first] = i, idxs[ne.first] = ne.second;
            for(pair<int, int> &ne : G[E[i][1]]) {
                if(vis[ne.first] == i) {
                    nodes[ne.second].push_back(E[i][0]);
                    nodes[idxs[ne.first]].push_back(E[i][1]);
                    nodes[i].push_back(ne.first);
                }
            }
        }

        // 将三元环按顶点归类，每个顶点自动获得按权值和排序的边
        vector<int> C[N];
        for(int i = 0; i < M; ++i)
            for(int n : nodes[i])
                C[n].push_back(i);
        
        // 求出结果
        int res = 0;
        for(int i = 0; i < N; ++i) {
            int bound = (int)C[i].size() - 1;
            for(int a = 0; a < min(3, (int)C[i].size()) && bound >= a; ++a) {
                for(int b = a; b <= bound; ++b) {
                    int cur = W[i] + W[E[C[i][a]][0]] + W[E[C[i][a]][1]], cnt = 0;
                    if(E[C[i][b]][0] != E[C[i][a]][0] && E[C[i][b]][0] != E[C[i][a]][1])
                        cur += W[E[C[i][b]][0]], ++cnt;
                    if(E[C[i][b]][1] != E[C[i][a]][0] && E[C[i][b]][1] != E[C[i][a]][1])
                        cur += W[E[C[i][b]][1]], ++cnt;
                    res = max(res, cur);
                    // if(cnt == 2) {
                    //     bound = b-1;
                    //     break;
                    // }
                }
            }
        }
        return res;
    }
};

数组第 k 大子序列和

2386. 找出数组的第 K 大和 数据范围：n 1e5，值域 [-1e9, 1e9]，k 不超过 2000

• 简化版：给定非负数组，按升序排列，求 k 小子序和

用最短路模型建模：每个子序列看成一个节点，比如说 a[p1]a[p2]...a[pm]，然后连边，跟 a[p1]a[p2]...a[pm]a[pm+1] 和 a[p1]a[p2]...a[pm-1]a[pm+1] 各连一条有向边，边权为子序列和的差，即 a[pm+1] 和 a[pm+1]-a[pm]，会得到一个有向图，边权都是非负的，a[1] 对应源点，跟所有子序列都存在路径，那么本题可看成是在图上跑 dijkstra 算法

因此做法就是：用最小堆，维护 (s,i)，每次出堆后，把 (s+a[i+1],i+1) 和 (s+a[i+1]-a[i],i+1) 入堆，对应上述连边的过程。第 k-1 次出堆就是答案，因为第一次总是空集

• 最小和怎么转化为最大和？

用 sum-res 就行了，这是一个 bijection

• 有负数怎么办？

求出负数的和，把负数变正数，最后返回 neg+sum-res 即可

为什么：这样得到的每个序列唯一对应一个原序列：对于所有在该子序列中的非负数，令它成为答案的一部分；对于所有不在该子序列中的负数，令它成为答案的一部分。所以也是一个 bijection

class Solution {
public:
    long long kSum(vector<int>& nums, int k) {
        int n = nums.size();
        LL sum = 0, neg = 0;
        for (int& x: nums)
        {
            if (x < 0) neg += x, x = -x;
            sum += x;
        }
        sort(nums.begin(), nums.end());
        
        LL res = 0;
        priority_queue<PLI, vector<PLI>, greater<PLI>> q;
        q.push({nums[0], 0});
        for (int i = 2; i <= k; i++)
        {
            PLI p = q.top();
            q.pop();
            res = p.x;
            if (p.y == n - 1) continue;
            q.push({p.x + nums[p.y + 1], p.y + 1});
            q.push({p.x - nums[p.y] + nums[p.y + 1], p.y + 1});
        }
        return neg + (sum - res);
    }
};

两数组和最小的 k 对数字

373. 查找和最小的 K 对数字 给定两个以 非递减顺序排列 的整数数组 nums1 和 nums2 , 以及一个整数 k。 定义一对值 (u,v)，其中第一个元素来自 nums1，第二个元素来自 nums2。 请找到和最小的 k 个数对 (u(1),v(1)), (u(2),v(2)) ... (u(k),v(k)) 。 数据范围 1e5，值域 [-1e9, 1e9]，k 1e4

此为上面的类似题型，也是用堆来做，最小的肯定是 (a[0],b[0])，我们可以出堆之后，把 (a[1],b[0]) 和 (a[0],b[1]) 入堆，但问题是 (a[1], b[1]) 会被入堆两次，怎么办？

用哈希表记录下哪些下标对在堆中咯！可以，但有更简单的做法

强制规定 (i,j-1) 出堆时，把 (i,j) 入堆，那么 (i-1,j) 时不做事，可以！不过此时发现，(1,0) (2,0) 这些没人更新了！因此我们要提前把这些数对都入堆

class Solution {
public:
    vector<vector<int>> kSmallestPairs(vector<int> &nums1, vector<int> &nums2, int k) {
        vector<vector<int>> ans;
        priority_queue<tuple<int, int, int>> pq; // (a[i]+b[j], i, j)
        int n = nums1.size(), m = nums2.size();
        for (int i = 0; i < min(n, k); i++) // 至多 k 个
            pq.emplace(-nums1[i] - nums2[0], i, 0); // 取相反数变成小顶堆
        while (!pq.empty() && ans.size() < k) {
            auto [_, i, j] = pq.top();
            pq.pop();
            ans.push_back({nums1[i], nums2[j]});
            if (j + 1 < m)
                pq.emplace(-nums1[i] - nums2[j + 1], i, j + 1);
        }
        return ans;
    }
};

用积木填满网格的可行性问题

从原神 4.5 版本活动中抽象出来的题 给定 n×n 网格（n 是奇数），有四种不同的积木，输入一个坐标 (x,y)，表示初始时这个格子被堵住了，返回 true 或 false，表示是否存在一种方案，可以用任意的积木，把剩余的网格填满（数据范围 n<1e18）

分析：这种用特定形状填充网格的可行性问题，要想到涂色的思想：即把网格按照黑白相间涂色（如下图），发现 黑色格子数=白色格子数+1，再观察积木形状，发现无论积木怎么摆，填充的黑色格一定等于白色格。因此，只要被 ban 的是黑色格，剩余的黑=白，一定有解，否则无解。直接返回 (x+y)%2==0 即可

二分本质相关的题

https://codeforces.com/contest/1945/problem/E 给定长为 n 的排列及 x，定义二分操作

int l = 1, r = n + 1;
while (r - l > 1) {
    int m = (l + r) / 2;
    if (p[m] <= x) l = m;
    else r = m;
}

可以证明最多一次交换就可以使得最后得到的 a[l]==x，给出交换的下标

做法是容易的，对原数组跑一遍这个二分，得到的 l 跟原本 x 的位置 p 交换即可

怎么证明及思考呢？

• 若 a[l]==x，刚刚好
• 若小于，根据循环不变量的知识，原来二分到 l 的过程在交换后还是会二分到 l（不好用文字表达，但可以 get 到意思）
• 若大于，最后的 l 一定是 1，因为只有每次 a[m] 都大于 x 才不断减小右端点（或者知道这个模板是开区间二分的话，就知道 1 是在区间以外了，不知道这样说对不对），而且若 l 不是 1，则一定被当成 m 检查过。将 x 与第一个元素交换不会影响二分的过程

导弹拦截与 Dilworth 定理

导弹拦截问题是说一个拦截系统只能拦截一个非递增子序列，问给定数组最少需要多少个拦截系统，也即是说：数组分成不交的非递增子序列，最少分几个

Dilworth 定理是说：偏序集最少的链划分数等于其最长反链长度

为什么 S-D 最长反链是 k-1，因为 C[i] 中所有属于长为 k 的反链的元素都被 D 挖走了，剩下的最多也是 k-1

所以根据这个定理，想知道最少分几个就等价于求最长递增子序列长度！

一个与将区间同余转换到 gcd trick

https://codeforces.com/contest/1548/problem/B

如果同余，那么 ，这就转化到 差分 + 区间 gcd 了，用 ST 表在差分数组上求最长的 gcd>1 的区间，二分区间长度，枚举区间起点，就解决了

void init() {
    for (int i = 1; i < n; i++) {
        rmq[i][0] = abs(a[i] - a[i + 1]); // 数组下标是 [1,n]，但不处理 a[n]
        if (i == 1) {
            lg[i] = 0;
        } else {
            lg[i] = lg[i >> 1] + 1;
        }
    }
    for (int p = 1, len = 2; p <= 20; p++, len <<= 1) {
        for (int i = 1; i + len - 1 < n; i++) {
            rmq[i][p] = gcd(rmq[i][p - 1], rmq[i + len / 2][p - 1]);
        }
    }
}
 
LL query(int l, int r) {
    int p = lg[r - l + 1];
    return gcd(rmq[l][p], rmq[r - (1 << p) + 1][p]);
}
 
bool check(int mid) {
    for (int i = 1; i + mid - 1 < n; i++) { // 注意范围
        if (query(i, i + mid - 1) != 1LL) {
            return true;
        }
    }
    return false;
}

        int l = 0, r = n - 1;
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (check(mid)) {
                l = mid;
            } else {
                r = mid - 1;
            }
        }
        cout << l + 1 << endl; // 最后输出 l+1，最短的区间是 1

函数调用（拓扑 + 数学）

https://www.luogu.com.cn/problem/P7077

给你一些计算：+1 *2 +3 *4 ... 怎么计算最终得到的值？

思路大概就是倒着遍历这些操作，维护一个乘法系数，每遇到一个 +x，实际加的是 x*mul

这题因为有多重调用，联想到图论，连边 + 拓扑，父节点的 mul 等于子节点的 mul 之积

struct Node {
    int type, idx;
    LL v, mul, sum;
} b[N];

void getMul() { // 计算乘法的系数
    for (int i = m; i; i--) {
        int x = q[i];
        for (int y: g[x]) {
            b[x].mul = b[x].mul * b[y].mul % mod;
        }
    }
}

void getSum() {
    for (int i = 1; i <= m; i++) {
        int x = q[i];
        LL now = 1;
        for (int i = g[x].size() - 1; i >= 0; i--) {
            int y = g[x][i];
            b[y].sum = (b[y].sum + b[x].sum * now % mod) % mod;
            now = now * b[y].mul % mod;
        }
    }
}

    topsort();
    getMul();
    cin >> Q;
    LL now = 1;
    for (int i = 1; i <= Q; i++) {
        cin >> f[i];
    }
    for (int i = Q; i; i--) {
        int x = f[i];
        b[x].sum = (b[x].sum + now) % mod;
        now = now * b[x].mul % mod;
    }
    getSum();
    for (int i = 1; i <= n; i++) {
        a[i] = a[i] * now % mod;
    }
    for (int i = 1; i <= m; i++) {
        if (b[i].type == 1) {
            a[b[i].idx] = (a[b[i].idx] + b[i].v * b[i].sum % mod) % mod;
        }
    }

离线询问 [l,r] 不同元素个数

给定数组和若干询问，每次回答 [l,r] 有几种不同的数。

对于给定的区间，我们只关心每个数出现的最右位置。因此思路是离线查询，将所有区间按右端点排序，从左到右遍历每个查询，用树状数组维护这些「最右位置」，区间和就是答案

    sort(q, q + m, [](Node &A, Node &B) {
        return A.y < B.y;
    });
    for (int i = 0, j = 1; i < m; i++) {
        while (j <= q[i].y) {
            if (p[a[j]]) {
                add(p[a[j]], -1);
            }
            add(j, 1);
            p[a[j]] = j;
            j ++;
        }
        res[q[i].idx] = query(q[i].y) - query(q[i].x - 1);
    }

区间合并技巧

有 n 个城市，编号从 0 到 n - 1。初始时，每个城市 i 都有一条单向道路通往城市 i + 1（ 0 <= i < n - 1）。

queries[i] = [ui, vi] 表示新建一条从城市 ui 到城市 vi 的单向道路。每次查询后，你需要找到从城市 0 到城市 n - 1 的最短路径的长度。

所有查询中不会存在两个查询都满足 queries[i][0] < queries[j][0] < queries[i][1] < queries[j][1]。

返回一个数组 answer，对于范围 [0, queries.length - 1] 中的每个 i，answer[i] 是处理完前 i + 1 个查询后，从城市 0 到城市 n - 1 的最短路径的长度。

题意指的是新加的边不会交叉，每次加边会合并一些区间

方法一：用 set 动态维护所有区间，it = st.erase(it) 删除当前元素并返回下一个元素的迭代器

class Solution {
public:
    using PII = pair<int, int>;
    vector<int> shortestDistanceAfterQueries(int n, vector<vector<int>>& queries) {
        set<PII> st;
        for (int i = 0; i < n - 1; i++) {
            st.insert({i, i + 1});
        }
        vector<int> res;
        for (auto &q: queries) {
            int l = q[0], r = q[1];
            auto it = st.lower_bound({l, -1});
            if (it != st.end() && it->first == l && it->second < r) {
                while (it != st.end() && it->first < r) {
                    it = st.erase(it);
                }
                st.insert({l, r});
            }
            res.push_back(st.size());
        }
        return res;
    }
};

方法二：用并查集维护，连通块数量就是最短长度

class Solution {
public:
    vector<int> shortestDistanceAfterQueries(int n, vector<vector<int>>& queries) {
        vector<int> p(n - 1);
        for (int i = 0; i < n - 1; i++) {
            p[i] = i;
        }
        
        auto find = [&](int x) -> int {
            int root = x;
            while (p[root] != root) {
                root = p[root];
            }
            while (p[x] != root) {
                int tmp = p[x];
                p[x] = root;
                x = tmp;
            }
            return root;
        }; // 递归版的也可以
        
        vector<int> res;
        int cnt = n - 1;
        for (auto &q: queries) {
            int l = q[0], r = q[1] - 1;
            int root = find(r);
            for (int i = find(l); i < r; i = find(i + 1)) {
                p[i] = root;
                cnt --;
            }
            res.push_back(cnt);
        }
        return res;
    }
};

方法三：线段树，一开始全为 1，合并的区间内的点置 0，区间和即为答案

const int N = 100010;
class Solution {
public:
    struct Node {
        int l, r, val;
    };
    Node tr[N << 2];
    void build(int u, int l, int r) {
        tr[u] = {l, r};
        if (l == r) {
            tr[u].val = 1;
            return;
        }
        int mid = l + r >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
        tr[u].val = tr[u << 1].val + tr[u << 1 | 1].val;
    }
    void update(int u, int L, int R) {
        if (tr[u].val == 0) { // 不加这个的话就需要懒标记下传
            return;
        }
        if (L <= tr[u].l && tr[u].r <= R) {
            tr[u].val = 0;
            return;
        }
        int mid = tr[u].l + tr[u].r >> 1;
        if (L <= mid) {
            update(u << 1, L, R);
        }
        if (R > mid) {
            update(u << 1 | 1, L, R);
        }
        tr[u].val = tr[u << 1].val + tr[u << 1 | 1].val;
    }
    vector<int> shortestDistanceAfterQueries(int n, vector<vector<int>>& queries) {
        build(1, 1, n - 1);
        vector<int> res;
        for (auto &q: queries) {
            update(1, q[0] + 2, q[1]);
            res.push_back(tr[1].val);
        }
        return res;
    }
};