钱力古的小博客

切换主题

模拟进制转换 ​

把十进制字符串转换为 进制的结果，可以结合竖式除法来理解下面的代码

cpp
// 把十进制字符串 s 转成 b 进制
// 用小学学过的【竖式除法】计算，读者可以先用竖式除法算算 1234÷10，再对照下面的代码
vector<int> trans(string& s, int b) {
    for (char& c : s) {
        c -= '0';
    }
    vector<int> digits;
    while (!s.empty()) {
        string nxt_s; // 用竖式除法计算 s / b 得到的商（十进制）
        int rem = 0; // s % b
        for (char c : s) {
            rem = rem * 10 + c;
            int q = rem / b; // 商
            if (q || !nxt_s.empty()) {
                nxt_s.push_back(q);
            }
            rem = rem % b;
        }
        digits.push_back(rem);
        s = move(nxt_s);
    }
    ranges::reverse(digits);
    return digits;
}

扫描线+线段树求矩形面积的并集 ​

题源 LC850，给定若干个二维平面上的矩形，求出总面积，重叠部分算一次

考虑一条平行于 轴的扫描线，所有被覆盖到的区间构成了当前的底边长，每次扫描的时候都会加入/移除一些区间，考虑用线段树维护这些区间的总长

其实我们并不关心每个点的 值，把所有 值离散化之后，区间长度就是 ，那么不如直接维护这 个点所构成的 个区间，每次操作会把一段连续区间的覆盖数 或

然后出现了一个难点：每次计算底边长的时候需要知道所有覆盖值大于 的区间和，怎么用线段树维护这个信息？

注意，这里不可以直接维护这个区间和，因为每次对一段连续区间执行操作之后，内部有些区间覆盖值大于 ，有些可能减为 ，说明这个操作对元素会有不同的影响。我们需要维护那些对于所有元素都有相同影响的操作

技巧：维护覆盖值的最小值 ，以及满足覆盖值等于 的区间和 。这样的好处是：每次执行 操作，只会影响 ，不影响 。如何求目标区间和？设区间总长为 ，当 时，答案为 ，否则答案为

使用懒标记下推的线段树维护即可

cpp
class Solution {
public:
    int rectangleArea(vector<vector<int>>& rectangles) {
        int n = rectangles.size(), m = 0;
        map<int, int> mp;
        for (auto &r : rectangles) {
            mp[r[0]] = mp[r[2]] = 1;
        }
        for (auto &p : mp) {
            p.second = m ++;
        }
        int A[m];
        for (auto &p : mp) {
            A[p.second] = p.first;
        }

        struct Node {
            // mn：当前节点的最小覆盖数
            // len：满足覆盖数 = 最小覆盖数的 A[i] 之和
            // lazy：加法的懒标记
            int mn, len, lazy;

            // 对节点的覆盖数整个增加 qv，只影响 mn，不影响 len
            void add(int qv) {
                mn += qv;
                lazy += qv;
            }
        } tree[m * 4 + 5];

        // 线段树两个子节点合并
        auto merge = [&](Node &nl, Node &nr) {
            int mn = min(nl.mn, nr.mn);
            return Node {
                mn,
                (nl.mn == mn ? nl.len : 0) + (nr.mn == mn ? nr.len : 0),
                0
            };
        };

        // 线段树模板开始

        // 建树
        auto build = [&](this auto &&self, int id, int l, int r) -> void {
            if (l == r) {
                // 区间长度
                tree[id] = { 0, A[r] - A[r - 1], 0 };
            }
            else {
                int nxt = id << 1, mid = (l + r) >> 1;
                self(nxt, l, mid); self(nxt | 1, mid + 1, r);
                tree[id] = merge(tree[nxt], tree[nxt | 1]);
            }
        };

        // 懒标记下推
        auto down = [&](int id) {
            if (tree[id].lazy == 0) {
                return;
            }
            int nxt = id << 1;
            tree[nxt].add(tree[id].lazy);
            tree[nxt | 1].add(tree[id].lazy);
            tree[id].lazy = 0;
        };

        // 区间加减覆盖次数
        auto modify = [&](this auto &&self, int id, int l, int r, int ql, int qr, int qv) -> void {
            if (ql <= l && r <= qr) {
                tree[id].add(qv);
            }
            else {
                down(id);
                int nxt = id << 1, mid = (l + r) >> 1;
                if (ql <= mid) {
                    self(nxt, l, mid, ql, qr, qv);
                }
                if (qr > mid) {
                    self(nxt | 1, mid + 1, r, ql, qr, qv);
                }
                tree[id] = merge(tree[nxt], tree[nxt | 1]);
            }
        };

        // 线段树模板结束

        // 把矩形的上下边界取出来
        vector<array<int, 4>> vec;
        for (auto &r : rectangles) {
            // y, x1 和 x2 所覆盖的区间(+1 是因为区间计数从 1 开始),qv
            vec.push_back({r[1], mp[r[0]] + 1, mp[r[2]], 1});
            vec.push_back({r[3], mp[r[0]] + 1, mp[r[2]], -1});
        }
        sort(vec.begin(), vec.end());

        // 求总的面积并
        long long tot = 0;
        build(1, 1, m - 1);
        for (int i = 0; i + 1 < vec.size(); i++) {
            // 考虑水平线 y = vec[i][0] 和 y = vec[i + 1][0] 之间的情况
            modify(1, 1, m - 1, vec[i][1], vec[i][2], vec[i][3]);
            // 求横截长度
            int len = A[m - 1] - A[0];
            // 如果最小覆盖数是 0，那么扣掉相应的长度
            if (tree[1].mn == 0) {
                len -= tree[1].len;
            }
            // 面积 = 横截长度 * 高度差
            tot += 1LL * len * (vec[i + 1][0] - vec[i][0]) % 1000000007;
        }
        return tot % 1000000007;
    }
};

曼哈顿距离转化为切比雪夫距离 ​

如何计算点对间的最大曼哈顿距离？

首先

不妨暴力枚举四种选法，可以总结为

即对于点 ，设 ，，那么距离为 和 的最大值。排序之后最值相减即可

结论：曼哈顿距离在坐标轴旋转 45 度后与切比雪夫距离等价

包含「子数组长度」的式子的处理技巧 ​

例题为 ABC146E，求出有多少个子数组满足：sum(b) % k = len(b)。可以转化为 sum(b-1) % k = 0，然后就是常见的处理方法了

当然，转化之后的计算要结合题目条件，例如本题，式子成立的条件为 0<=len(b)<=k-1，在使用前缀和时要剔除窗口以外的值

容斥原理计算 [l,r] 内的区间个数 ​

先读入若干区间，然后每次询问回答 内有多少个闭区间

计算公式为 f[l][r] = f[l+1][r]+f[l][r-1]-f[l+1][r-1]+cnt[l][r]

cpp
        int f[n + 2][n + 2];
        memset(f, 0, sizeof(f));
        for (int i = 0, l, r; i < m; i++) {
            cin >> l >> r;
            f[l][r] ++;
        }
        for (int l = n; l; l--) {
            for (int r = l + 1; r <= n; r++) {
                f[l][r] += f[l + 1][r] + f[l][r - 1] - f[l + 1][r - 1];
            }
        }

双单调栈求左边更大元素以及更更大元素 ​

模板见 LC2454

应用见 ABC140E

cpp
        auto calc = [&](int start, int d, vector<int> &nxt, vector<int> &nxt2) {
            vector<int> st1, st2;
            for (int i = start; i >= 0 && i < n; i += d) {
                int x = a[i];
                while (st2.size() && a[st2.back()] < x) {
                    nxt2[st2.back()] = i; // st2 栈顶的下下个更大元素是 x
                    st2.pop_back();
                }
                int j = st1.size();
                while (j && a[st1[j - 1]] < x) {
                    nxt[st1[j - 1]] = i; // st1 栈顶的下一个更大元素是 x
                    j --;
                }
                st2.insert(st2.end(), st1.begin() + j, st1.end()); // 把从 st1 弹出的这一整段元素加到 st2
                st1.resize(j); // 弹出一整段元素
                st1.push_back(i); // 当前元素（的下标）加到 s 栈顶
            }
        };

组合计数中任意插入字符时去重的技巧 ​

给定串 ，任意插入 个字符，求方案数

去重技巧：做一个规定，插入在 左侧的字符，不能和 相同，这不会影响答案的正确性

枚举最后一个字符的右侧插入了多少个字符，设为 ，这些字符没有限制，有 种方案

剩下 个字符，我们需要考虑其中 个字符的位置，这就是

因此方案数就是

构造排列使得 gcd(i,a[i]) 之和为 k ​

的范围为 时有解

观察：如果 比较大，可以让 ，转化为子问题

分界点是什么？剩下 个数，最少贡献 ，因此分界点可以为

如果 较小时，可以让 ，转化为子问题

边界情况：列出 、、 时的所有状态看看，发现 和 时用这种构造解决不了，因此需要特判。当 时，所有取值都可以转移到已经被解决的子问题

cpp
std::vector<int> construct(int n, i64 k) {
    std::vector<int> p;
    if (n == 0) {
         
    } else if (n == 1) {
        p = {1};
    } else if (n == 3 && k == 4) {
        p = {3, 2, 1};
    } else if (n == 4 && k == 6) {
        p = {3, 4, 1, 2};
    } else if (k >= 2 * n - 1) {
        p = construct(n - 1, k - n);
        p.push_back(n);
    } else {
        p = construct(n - 2, k - 2);
        p.push_back(n);
        p.push_back(n - 1);
    }
     
    return p;
}

树上滑窗例题 ​

题源 LC3425，给定一棵树，求出最长路径，使得路径中节点的点权互不相同

需要记录每种点权最近一次出现的深度，那么路径起点的深度，就是路径所有点权的最近出现深度的最大值

用一个哈希表记录每种点权最近出现的深度，用一个栈维护根节点到 DFS 节点的路径长度，那么路径长度可以通过作差得到

cpp
    vector<int> nums;
    vector<vector<PII>> g;
    PII res = {-1, 0};
    vector<int> dis = {0};
    unordered_map<int, int> last_dep; // 最近出现深度的最大值 +1
    void dfs(int u, int fa, int tot_dep) {
        int color = nums[u];
        int old_dep = last_dep[color];
        tot_dep = max(tot_dep, old_dep);

        // 这里还要求最长路径的最小节点数，就是 dis.size() - tot_dep - 1，为了方便处理，变成相反数
        res = max(res, pair(dis.back() - dis[tot_dep], tot_dep - (int)dis.size()));

        last_dep[color] = dis.size();
        for (auto &[v, w]: g[u]) {
            if (v != fa) {
                dis.push_back(dis.back() + w); // 把根节点到每个节点的距离入栈
                dfs(v, u, tot_dep);
                dis.pop_back();
            }
        }
        last_dep[color] = old_dep;
    }

进阶版题源 LC3486，允许路径上只有一个点权出现两次。需要额外维护这个重复点权出现的更靠上的深度，其余逻辑不用变

cpp
    vector<int> nums;
    vector<vector<PII>> g;
    PII res = {-1, 0};
    vector<int> dis = {0};
    unordered_map<int, int> last_dep; // 最近出现深度 +1
    void dfs(int u, int fa, int tot_dep, int last1) {
        int color = nums[u];
        int last2 = last_dep[color];
        // 更新时需要比较 维护的重复点权 和 当前点权 的出现情况
        tot_dep = max(tot_dep, min(last1, last2));

        res = max(res, pair(dis.back() - dis[tot_dep], tot_dep - (int)dis.size()));

        last_dep[color] = dis.size();
        for (auto &[v, w]: g[u]) {
            if (v != fa) {
                dis.push_back(dis.back() + w);
                dfs(v, u, tot_dep, max(last1, last2)); // last1 的更新逻辑
                dis.pop_back();
            }
        }
        last_dep[color] = last2;
    }

不重叠区间，定长窗口能覆盖的最多下标数量 ​

题源 LC2271 以及 LC3413

可以发现窗口右端点在区间内部，可以转化为对齐区间的右端点，这样做答案不会变少，因此可以排序之后双指针

固定 之后，窗口左端点在 处，窗口外的区间满足 ，据此来移动指针

cpp
class Solution {
public:
    int maximumWhiteTiles(vector<vector<int>>& tiles, int carpetLen) {
        ranges::sort(tiles, {}, [](auto &t) { return t[0]; });
        int res = 0, cnt = 0, l = 0;
        for (auto &t: tiles) {
            int tl = t[0], tr = t[1];
            cnt += tr - tl + 1;
            while (tiles[l][1] < tr - carpetLen + 1) {
                cnt -= tiles[l][1] - tiles[l][0] + 1;
                l ++;
            }
            int uncover = max(0, tr - carpetLen + 1 - tiles[l][0]);
            res = max(res, cnt - uncover);
        }
        return res;
    }
};

进阶版本是：每个区间给定权重，区间内部每个坐标的权值相等，求最大权值和

这里就要分对齐左端点和对齐右端点分别讨论了，因为左边区间的权值可能大于右边区间

做法就是反转区间，把 变成 ，就可以复用右端点对齐的代码了

cpp
class Solution {
public:
    using LL = long long;
    long long maximumCoins(vector<vector<int>>& coins, int k) {
        auto calc = [&]() {
            LL res = 0, cnt = 0;
            int l = 0;
            for (auto &t: coins) {
                int tl = t[0], tr = t[1], c = t[2];
                cnt += 1LL * (tr - tl + 1) * c;
                while (coins[l][1] < tr - k + 1) {
                    cnt -= 1LL * (coins[l][1] - coins[l][0] + 1) * coins[l][2];
                    l ++;
                }
                LL uncover = max(0LL, 1LL * (tr - k + 1 - coins[l][0]) * coins[l][2]);
                res = max(res, cnt - uncover);
            }
            return res;
        };
        
        ranges::sort(coins, {}, [](auto &t) { return t[0]; });
        LL res = calc();
        ranges::reverse(coins);
        for (auto &t: coins) {
            int x = t[0];
            t[0] = -t[1];
            t[1] = -x;
        }
        return max(res, calc());
    }
};

哈希表维护 a[p] * a[r] == a[q] * a[s] ​

给数组，问满足条件的下标对数 ，将 变形为 ，这样可以前后缀分解

怎么维护这个分数呢？将 变为最简分数，做法是同除它们的 GCD，然后插入哈希表中。如何插入？分子分母映射为一个 key 值即可

什么时候能直接用浮点数来表示？当 时就不行了

此技巧来自于 LC3404题解

求字符串字典序最大的子串 ​

模板和证明在 LC1163官解

首先一定是后缀才有可能成为最大的子串，采用双指针的思路， 指向当前已知最大的子串， 指向当前在比较的子串开头，一直找到第一个不同的字符，根据 和 的大小来确定下一个比较的串，在这个过程中可以发现一些性质来跳过一些串

cpp
class Solution {
public:
    string lastSubstring(string s) {
        int i = 0, j = 1, n = s.size();
        while (j < n) {
            int k = 0;
            while (j + k < n && s[i + k] == s[j + k]) {
                k ++;
            }
            if (j + k < n && s[i + k] < s[j + k]) {
                int t = i;
                i = j;
                j = max(j + 1, t + k + 1);
            } else {
                j = j + k + 1;
            }
        }
        return s.substr(i, n - i);
    }
};

找字典序最小的子串的思路也是一样的，时间复杂度

负数取模的知识 ​

这里讨论的是被除数为负数，除数为正数的情况，例如

很多时候需要维护形如 的情况，枚举 的时候，需要找到 的 ，那么哈希表如何记录 key 呢

如果是 Python 的话可以直接负数取模，结果是正数。而在 C++ 的默认模运算中，负数取模后是负数，这会导致结果错误。为什么？由同余定理，，那么就有 ，但是如果算成负数的话，，就违反定理了

其实结果取正取负都可以解释，例如 -17=10*(-2)+3 也等于 -17=10*(-1)+(-7)，但取正数才符合实际

如何转换成正数： 写成 即可

001110 最小交换次数变成 010101 ​

对于这种交错的 ，首先要讨论交换成 和 两种情况

定理：如果有 个位置与目标不同，需要交换 次即可

首先因为 是下限，然后证明可以用这么多次交换做到

详细证明可以分 的奇偶性讨论，然后讨论多少个 在奇数下标上，多少 在偶数下标上，据此推出交换次数

判断平面上点组成矩阵的最大面积 ​

限制是不能有其它点在矩形区域内，包括边界

暴力的 做法是枚举左上和右下端点，再遍历所有点去 check

使用扫描线思想，枚举竖线，这条线上的每一对相邻点都判断一次，核心是使用哈希表，其中 key 为 ya << 32 | yb，找到最靠近的相同 key 对应的 值，矩形的长就知道了

接下来是判断这个区域内有没有点，还是得用离散化树状数组，满足两条竖线左边的满足 的点数只差等于 的话就是合法的，这里的 就是矩形左边界的两个端点

所对应的满足 的点数可以顺便在哈希表中记录，因此用一个 pair 作为 value

cpp
class Solution {
public:
    using LL = long long;
    using PII = pair<int, int>;
    long long maxRectangleArea(vector<int>& xs, vector<int>& ys) {
        int n = xs.size(), m = 0;
        map<int, int> mp;
        for (int y: ys) {
            mp[y] = 1;
        }
        for (auto &p: mp) {
            p.second = ++ m;
        }
        
        map<int, vector<PII>> vs;
        for (int i = 0; i < n; i++) {
            vs[xs[i]].push_back({mp[ys[i]], i});
        }
        for (auto &[_, t]: vs) {
            ranges::sort(t);
        }
        
        int tr[m + 1];
        memset(tr, 0, sizeof(tr));
        auto add = [&](int x, int v) {
            for (int i = x; i <= m; i += i & -i) {
                tr[i] += v;
            }
        };
        auto query = [&](int x) {
            int res = 0;
            for (int i = x; i; i -= i & -i) {
                res += tr[i];
            }
            return res;
        };
        
        LL res = -1;
        map<LL, PII> last;
        for (auto &p: vs) {
            auto &v = p.second;
            for (int i = 0; i < v.size(); i++) {
                if (i == 0) {
                    continue;
                }
                
                int ya = ys[v[i - 1].second], yb = ys[v[i].second];
                LL key = ((LL)ya << 32) | yb;
                // 假设现在的竖线是 x = t，这里用树状数组求满足 x < t，且 ya <= y <= yb 的点有几个
                int cnt = query(v[i].first) - query(v[i - 1].first - 1);
                if (last.count(key)) {
                    // oldX：矩形左边界的 x 坐标
                    // oldCnt：满足 x < oldX，且 ya <= y <= yb 的点有几个
                    auto &[oldCnt, oldX] = last[key];
                    // cnt - oldCnt 就是满足 oldX <= x < t 且 ya <= y <= yb 的点有几个
                    // 根据题意，这里要算出 2 才是合法的矩形，这个 2 就是矩形的左上和左下两个顶点
                    if (cnt - oldCnt == 2) {
                        res = max(res, 1LL * (p.first - oldX) * (yb - ya));
                    }
                }
                last[key] = {cnt, p.first};
            }
            for (auto &[x, _]: v) {
                add(x, 1);
            }
        }
        return res;
    }
};

gcd/lcm + 并查集 ​

LC3378 时连边，求连通块

思路是转换为 gcd，枚举 ，找到数组中最小的 的倍数 ，然后把 都并起来

LC2709 时连边，判断连通性

把每个数都和所有质因子并起来

LC1627 和 存在大于 的因子时连边，判断连通性

枚举大于 的数 ，把 的倍数都并起来

统计和为正数的子数组 ​

分组循环模板 ​

适用场景： 按照题目要求，数组会被分割成若干组，且每一组的判断/处理逻辑是一样的

核心思想：

  • 外层循环负责遍历组之前的准备工作（记录开始位置），和遍历组之后的统计工作（更新答案最大值）
  • 内层循环负责遍历组，找出这一组最远在哪结束
cpp
// 分组循环
// 外层循环 枚举子数组的起点
// 内层循环 扩展子数组的右端点
int ans = 0, i = 0;
while (i < n) {
    if (nums[i] > threshold || nums[i] % 2) {
        i++; // 直接跳过
        continue;
    }
    int start = i; // 记录这一组的开始位置
    i++; // 开始位置已经满足要求，从下一个位置开始判断
    while (i < n && nums[i] <= threshold && nums[i] % 2 != nums[i - 1] % 2) {
        i++;
    }
    // 从 start 到 i-1 是满足题目要求的（并且无法再延长的）子数组
    ans = max(ans, i - start);
}
return ans;

[new]：可以用分组循环写一段求出数组峰值峰谷元素（包含首尾）的代码（我自己写的）

cpp
for (int i = 0; i < n; ) {
    ans.push_back(a[i]);
    i ++;
    int t = 0;
    for (; i < n && (t == 0 || (a[i] - a[i - 1]) * t > 0); i++) {
        if (t == 0) {
            t = (a[i] - a[i - 1] > 0 ? 1 : -1);
        }
    }
    if (t != 0) {
        i --;
    }
}

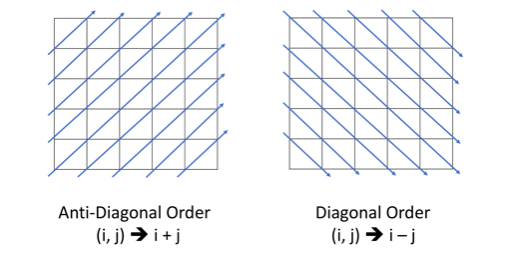
遍历矩阵每一条从左下到右上的斜对角线 ​

cpp
// 按斜线遍历
for (int i = 1; i < m + n - 2; i++)
{
    // ...
    for (int j = 0; j <= i; j++)
    {
        int x = j, y = i - j;
        if (x >= m || y >= n) continue;
        // ...
    }
    // ...
}

左上到右下不满足 x+y 为定值，枚举起点？

维护一个集合，支持动态求最值，删除和插入：multiset ​

注意一点， s.erase(val) 会删除所有等于 val 的值，而 s.erase(s.find(x)) 则只会删除一个 x ，求最小值用 *s.begin() ，最大值用 s.rbegin()

删除最后一个元素，要写 s.erase(prev(s.end())) 或者 s.erase(--s.end())

哈希表不能用 pair 作为 key ​

要么把 pair<x, y> 转成整数，如 1LL * x * n + y ，或者利用位运算，确保不冲突的情况下， key 变成 (LL)x << 32 | y

把有交集的区间合并在一个集合 统计集合数 ​

区间按左端点排序，遍历数组，同时维护区间右端点最大值

  • 如当前区间左端点大于 maxR，后面任何区间都不会和之前的区间有交集， cnt ++
  • 否则当前区间与上一个区间在同一个集合

区间选点 使得每个区间内至少包含一个选出的点 ​

按区间的右端点从小到大排序 每次总是选择当前区间的右端点

cpp
  int res = 0, ed = -2e9;
  for (int i = 0; i < n; i++)
    if (range[i].l > ed) {
      res++;
      ed = range[i].r;
    }

不重叠区间 ​

给定一些区间，选出若干不重叠的区间（只有一个点相交的不算），最多选多少

按右端点排序，选最左边的区间

cpp
    ranges::sort(intervals, {}, [](auto& a) { return a[1]; });
    int ans = 0;
    int pre_r = INT_MIN;
    for (auto& p : intervals) {
        if (p[0] >= pre_r) {
            ans++;
            pre_r = p[1];
        }
    }

K 个不同整数的子数组的数目 ​

用滑窗，枚举右端点，维护一段左端点的区间 [l1, l2) ，前者表示包含 k 个不同整数的区间的左端点，后者表示包含 k - 1 个不同整数的区间的右端点，每次答案加上 l2 - l1

对于维护窗口内不同整数个数的操作，如果值域较小可以用数组模拟，一般来说用哈希表模拟，善用 m.erase()

裴蜀定理推论 ​

引理：若一个环同时有一个长度为 的循环节（间隔为 的元素都相等），和一个长度为 的循环节，那么这个环有一个长度为 的循环节

对于一个长度为 的环，如果环上所有间隔为 的元素都要相等，那么环上所有间隔为 的元素都要相等

把序列元素变得相等的最小运算次数 ​

经典中位数贪心，把所有数变为中位数即可（见 最小操作次数使数组元素相等 II）

回文串判断 ​

cpp
// is_palindrome[l][r] 表示 s[l] 到 s[r] 是否为回文串
vector is_palindrome(n, vector<int>(n, true));
for (int l = n - 2; l >= 0; l--) {
    for (int r = l + 1; r < n; r++) {
        is_palindrome[l][r] = s[l] == s[r] && is_palindrome[l + 1][r - 1];
    }
}

回文串之中心扩散法 ​

不重叠回文子字符串的最大数目

cpp
class Solution {
public:
    int maxPalindromes(string s, int k) {
        int n = s.length(), f[n + 1];
        memset(f, 0, sizeof(f));
        for (int i = 0; i < 2 * n - 1; ++i) {
            // 更加优雅的方式枚举所有奇数和偶数的中心点位置
            int l = i / 2, r = l + i % 2; // 中心扩展法
            f[l + 1] = max(f[l + 1], f[l]);
            for (; l >= 0 && r < n && s[l] == s[r]; --l, ++r)
                if (r - l + 1 >= k) {
                    // 贪心处理，f[l]是非递减的，更小的f[l]也不会影响答案
                    f[r + 1] = max(f[r + 1], f[l] + 1);
                    break;
                }
        }
        return f[n];
    }
};

DFS序 ​

移除子树后的二叉树高度

cpp
class Solution {
    int n = 0, clk = 0;
    vector<int> A, L, R;

    void dfs(TreeNode *node, int d) {
        // 没有输入 n，只好动态计算 n 的大小并扩充列表...
        int idx = node->val;
        n = max(idx, n);
        while (A.size() <= n) A.push_back(0), L.push_back(0), R.push_back(0);

        // node 是第 clk 个被访问的点
        clk++;
        // A[i] 表示第 i 个被访问的点的深度
        A[clk] = d;
        // L[i] 表示第 i 个点的子树对应的连续区间的左端点
        L[idx] = clk;

        // DFS 子树
        if (node->left != nullptr) dfs(node->left, d + 1);
        if (node->right != nullptr) dfs(node->right, d + 1);

        // R[i] 表示第 i 个点的子树对应的连续区间的右端点
        R[idx] = clk;
    }

public:
    vector<int> treeQueries(TreeNode* root, vector<int>& queries) {
        dfs(root, 0);

        // f[i] 表示 max(A[1], A[2], ..., A[i])
        // g[i] 表示 max(A[n], A[n - 1], ..., A[i])
        vector<int> f(n + 2), g(n + 2);
        for (int i = 1; i <= n; i++) f[i] = max(f[i - 1], A[i]);
        for (int i = n; i > 0; i--) g[i] = max(g[i + 1], A[i]);

        vector<int> ans;
        // 树上询问转为区间询问处理
        for (int x : queries) ans.push_back(max(f[L[x] - 1], g[R[x] + 1]));
        return ans;
    }
};

统计 gcd 为 k 的子数组数目 ​

  1. 枚举子数组右端点，往左看有多少个不同的 gcd
  2. 如何优化：发现大量重复的 gcd
  3. 有多少个不同的 gcd ？由于 gcd 只会变小，且不超过原来的一半，故有 个 => 所有子数组至多有 个不同的 gcd
  4. 实现看代码
cpp
/*
	6 4 2 6 3
gcd:
	6
	2 4
	2 2 2
	2 2 2 6
	1 1 1 3 3
*/


class Solution {
public:
    int subarrayGCD(vector<int>& nums, int k) {
        int n = nums.size();
        int res = 0;
        vector<PII> a; // [gcd, 相同 gcd 的右端点]
        int i0 = -1; // 记录上一个不合法位置
        for (int i = 0; i < n; i++)
        {
            int x = nums[i];
            if (x % k) // 保证后续求的 gcd 都是 k 的倍数
            {
                a.clear();
                i0 = i;
                continue;
            }
            a.push_back({x, i});
            // 原地去重 因为相同的 gcd 都相邻
            int j = 0;
            for (PII& p: a)
            {
                p.x = gcd(p.x, x);
                if (a[j].x != p.x)
                {
                    j ++;
                    a[j].x = p.x, a[j].y = p.y;
                }
                else a[j].y = p.y;
            }
            a.erase(a.begin() + (j + 1), a.end());
            if (a[0].x == k) // a[0][0] >= k
                res += a[0].y - i0;
        }
        return res;
    }
};

给一个数 num 判断是否存在 k 使得 k + reverse(k) == num ​

cpp
class Solution {
public:
    bool sumOfNumberAndReverse(int num) {
        string s = to_string(num);
        function<bool(int,int,int,int)> f = [&](int i, int j, int pre, int suf) {
            if(i < j) {
                for(int m = 0, sum = pre * 10 + (s[i] - '0') - m; m <= 1; ++m, --sum)
                    if(sum >= int(i == 0) && sum <= 18 && (sum + suf) % 10 == s[j] - '0')
                        return f(i + 1, j - 1, m, (sum + suf) / 10);
                return false;
            }
            return (i == j && (s[i] & 1) == suf) || (i > j && pre == suf);
        };
        return f(0, s.size()-1, 0, 0) || (s[0]=='1' && f(1, s.size()-1, 1, 0));
    }
};

解法，思路见 题解

n=m=20,k=1e18，问从矩阵左上到右下的异或和等于 k 的路径数 ​

CF1006F，思路是折半枚举

cpp
map<LL, int> v[N][N];
int n, m, half;
LL k;
LL a[N][N];
LL res;

void dfs1(int x, int y, LL t, int cnt)
{
    t ^= a[x][y];
    if (cnt == half) 
    {
        v[x][y][t] ++;
        return;
    }
    if (x + 1 < n) dfs1(x + 1, y, t, cnt + 1);
    if (y + 1 < m) dfs1(x, y + 1, t, cnt + 1);
}

void dfs2(int x, int y, LL t, int cnt)
{
    if (cnt == n + m - 2 - half)
    {
        if (v[x][y].count(k ^ t)) 
            res += v[x][y][k ^ t];
        return;
    }
    if (x > 0) dfs2(x - 1, y, t ^ a[x][y], cnt + 1);
    if (y > 0) dfs2(x, y - 1, t ^ a[x][y], cnt + 1);
}

int main()
{
    scanf("%d%d%lld", &n, &m, &k);
    half = (n + m - 2) / 2;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < m; j++)
            scanf("%lld", &a[i][j]);
    
    dfs1(0, 0, 0, 0);
    dfs2(n - 1, m - 1, 0, 0);
    
    printf("%lld\n", res);
    return 0;
}

求 LCP 矩阵 ​

cpp
int lcp[n + 1][n + 1]; // lcp[i][j] 表示 s[i:] 和 s[j:] 的最长公共前缀
        memset(lcp, 0, sizeof(lcp));
        for (int i = n - 1; i >= 0; --i)
            for (int j = n - 1; j > i; --j)
                if (s[i] == s[j])
                    lcp[i][j] = lcp[i + 1][j + 1] + 1;

LCP 的性质 ​

给定字符串数组，任选 个串，最大的 LCP 是多少？

性质一：把字符串按字典序排序，那么答案一定在一个连续子数组内，考虑长度为 的子数组即可

性质二：子数组的 LCP，等价于首尾元素的 LCP。这一点可以通过证明 和 来证明，较为简单

区间分组，组内区间互不相交，最少组数 ​

经典贪心

cpp
class Solution {
public:
    int minGroups(vector<vector<int>>& intervals) {
        sort(intervals.begin(), intervals.end());
        // 维护一个小根堆表示所有组的结束时间
        priority_queue<int, vector<int>, greater<int>> pq;
        for (auto &vec : intervals) {
            // 判断是否存在一组（结束时间最小的组）使得它的结束时间小于当前区间的开始时间
            if (!pq.empty() && pq.top() < vec[0]) pq.pop();
            pq.push(vec[1]);
        }
        return pq.size();
    }
};

快速幂 ​

cpp
LL qmi(int a, int k, int p)
{
    LL res = 1;
    while (k)
    {
        if (k & 1) res = (LL)res * a % p;
        a = (LL)a * a % p;
        k >>= 1;
    }
    return res;
}
// 分子 * qmi(分母，mod - 2，mod)
cpp
LL qmi(LL a, int b)
{
    LL res = 1;
    for (; b; b /= 2)
    {
        if (n % 2) res = res * a % MOD;
        a = a * a % MOD;
    }
    return res;
}

字符串快速幂：假如指数是个字符串，怎么算呢？

比如说 x 的 456 次方，可以表示成 ，所以就可以线性遍历来计算了

cpp
    for (char c: p) {
      res = (qmi(res, 10, mod) * qmi(x, c - '0', mod)) % mod;
    }

next_permutation 的实现 ​

cpp
class Solution {
public:
    void nextPermutation(vector<int>& nums) {
        int i = nums.size() - 2;
        while (i >= 0 && nums[i] >= nums[i + 1]) i --;
        if (i >= 0)
        {
            int j = nums.size() - 1;
            while (j >= 0 && nums[i] >= nums[j]) j --;
            swap(nums[i], nums[j]);
        }
        reverse(nums.begin() + i + 1, nums.end());
    }
};

double 版快速幂 ​

cpp
class Solution {
public:
    typedef long long LL;
    double qmi(double x, LL n)
    {
        if (n == 0) return 1.0;
        double y = qmi(x, n / 2);
        return n % 2 == 0 ? y * y : y * y * x;
    }
    double myPow(double x, int n) {
        return n >= 0 ? qmi(x, (LL)n) : 1.0 / qmi(x, -(LL)n);
    }
};

遍历数组找到相邻元素和最小的对应下标 ​

还在想设 mx ？不需要！

cpp
int j = 1; // 设右端点
for (int i = 1; i < a.size(); i++)
    if (a[i] + a[i - 1] < a[j] + a[j - 1]) 
        j = i;

O(n^2) 离散化去重+二维差分模板 ​

见 最强祝福力场，就是给出若干矩形，问被矩形覆盖最多的点的被覆盖次数

遇到 0.5 就要乘以 2

cpp
class Solution {
public:
    int fieldOfGreatestBlessing(vector<vector<int>> &forceField) {
        // 1. 统计所有左下和右上坐标
        vector<long long> xs, ys;
        for (auto &f: forceField) {
            long long i = f[0], j = f[1], side = f[2];
            xs.push_back(2 * i - side);
            xs.push_back(2 * i + side);
            ys.push_back(2 * j - side);
            ys.push_back(2 * j + side);
        }

        // 2. 排序去重
        sort(xs.begin(), xs.end());
        xs.erase(unique(xs.begin(), xs.end()), xs.end());
        sort(ys.begin(), ys.end());
        ys.erase(unique(ys.begin(), ys.end()), ys.end());

        // 3. 二维差分
        int n = xs.size(), m = ys.size(), diff[n + 2][m + 2];
        memset(diff, 0, sizeof(diff));
        for (auto &f: forceField) {
            long long i = f[0], j = f[1], side = f[2];
            int r1 = lower_bound(xs.begin(), xs.end(), 2 * i - side) - xs.begin();
            int r2 = lower_bound(xs.begin(), xs.end(), 2 * i + side) - xs.begin();
            int c1 = lower_bound(ys.begin(), ys.end(), 2 * j - side) - ys.begin();
            int c2 = lower_bound(ys.begin(), ys.end(), 2 * j + side) - ys.begin();
            // 将区域 r1<=r<=r2 && c1<=c<=c2 上的数都加上 x
            // 多 +1 是为了方便求后面复原
            ++diff[r1 + 1][c1 + 1];
            --diff[r1 + 1][c2 + 2];
            --diff[r2 + 2][c1 + 1];
            ++diff[r2 + 2][c2 + 2];
        }

        // 4. 直接在 diff 上复原，计算最大值
        int ans = 0;
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= m; ++j) {
                diff[i][j] += diff[i - 1][j] + diff[i][j - 1] - diff[i - 1][j - 1];
                ans = max(ans, diff[i][j]);
            }
        }
        return ans;
    }
};

反悔贪心 ​

不能选相邻的，考虑 [8,9,8,1,2,3] ，一开始选了 9 ，不如选择两个 8 ，怎么办？

增加反悔操作，第一步选了 9 之后，要删除左右两个 8 ，但我们要把两个 8 的信息保存在 9 中，让后续有机会选到。具体地，把 9 的值更新成 8+8-9=7 。为什么这样？想想，后续选 7 的时候，原来两个 8 的左右不能选，因为此时 7 的左右就是原来 8 的左右，天然符合处理逻辑；并且这时得到 16 的同时我们也刚好选择了两次，即两个数，也符合选择了两个 8 ！

为什么我们的反悔操作一定是同时选择左右两个元素呢？因为我们是从大到小处理所有元素的，所以左右两边的元素一定不大于中间的元素，如果我们只选取其中的一个，是不可能得到更优解的。

例题：1388. 3n 块披萨

知识点：基于双向链表标记左右不能选，用堆实现贪心

cpp
struct Node {
    int v, l, r;
};
vector<Node> a;

struct Id {
    int id;
    bool operator<(const Id &t) const {
        return a[id].v < a[t.id].v;
    }
};

void del(int i)
{
    // 这里不需要更新i的左右指针，因为i已经不会再被使用了
    a[a[i].l].r = a[i].r;
    a[a[i].r].l = a[i].l;
}

class Solution {
public:
    int maxSizeSlices(vector<int>& slices) {
        int n = slices.size();
        int k = n / 3;
        a.clear();
        for (int i = 0; i < n; i++) a.push_back({slices[i], (i - 1 + n) % n, (i + 1) % n});
        priority_queue<Id> q;
        vector<bool> st(n, true);
        for (int i = 0; i < n; i++) q.push({i});
        int cnt = 0, res = 0;
        while (cnt < k)
        {
            int id = q.top().id;
            q.pop();
            if (st[id]) // 当前序号可用
            {
                cnt ++;
                res += a[id].v;
                // 标记前后序号
                int pre = a[id].l, nxt = a[id].r;
                st[pre] = 0, st[nxt] = 0;
                // 更新当前序号的值为反悔值
                a[id].v = a[pre].v + a[nxt].v - a[id].v;
                // 当前序号重新入队
                q.push({id});
                // 删除前后序号（更新双向链表）
                del(pre);
                del(nxt);
            }
        }
        return res;
    }
};

反悔贪心还有几道经典例题，比如630. 课程表 III，871. 最低加油次数，LCP 30. 魔塔游戏，2813. 子序列最大优雅度，共性是求一些限制下的最值。解法是以某种序关系进行遍历（模拟），必须用到一个堆，前面就贪心选，把选过的量存下来，当模拟过程中碰到限制时，取堆顶元素（相当于退回到那步反悔，把那一步操作了，当前就可以不操作了）更新当前的量，然后继续模拟下去

最近又做到几道相关的，都是 个物品，每个物品有多个属性，选一些获得 A 属性，另一些获得 B 属性，最大化收益。这种的做法就是无脑满足最大化选 A 的收益，然后用堆存反悔的贡献（例如 -a[i]+b[i]），再贪心地选 B 出来

异或的技巧 ​

前缀异或和

像构建回文串这样的需要统计字符出现次数的奇偶性的情况下，用前缀异或和，通常还要压缩成 mask 表示状态。

cpp
int main()
{
    cin >> s;
    cnt[0] = 1;
    for (int i = 0; i < s.size(); i++)
    {
        char c = s[i];
        mask ^= (1 << (c - '0'));
        res += cnt[mask];
        cnt[mask] ++;
    }
    cout << res << endl;
}

对于树上路径边权异或和，通常可以转化为 dist[i,j]=dist[1,i]^dist[1,j]，这里也是类似于前缀异或和的思想

如何计算数组中所有 a[i]^a[j] 之和呢？

拆位计算，假设有 个数满足第 位为 ，那么就对答案贡献

无向图定向 ​

把无向图所有边的方向定为从度数小的顶点指向度数大的顶点（相同则从节点编号小到大），任意点的度数不会超过 ，在一些需要多重循环枚举图中顶点的题中，定向后的复杂度变为

懒删除堆 ​

对于一些数据结构设计题，需要多次修改某个 key 对应的值，还要查询最大值/最小值，这种情况下用此技巧比较方便，修改的时候直接插入堆中并记录，查询的时候堆顶元素不同于记录值则弹出，否则就是答案

例题：2353. 设计食物评分系统

cpp
class FoodRatings {
    unordered_map<string, pair<int, string>> fs;
    unordered_map<string, priority_queue<pair<int, string>, vector<pair<int, string>>, greater<>>> cs;
public:
    FoodRatings(vector<string> &foods, vector<string> &cuisines, vector<int> &ratings) {
        for (int i = 0; i < foods.size(); ++i) {
            auto &f = foods[i], &c = cuisines[i];
            int r = ratings[i];
            fs[f] = {r, c};
            cs[c].emplace(-r, f);
        }
    }

    void changeRating(string food, int newRating) {
        auto &[r, c] = fs[food];
        cs[c].emplace(-newRating, food); // 直接添加新数据，后面 highestRated 再删除旧的
        r = newRating;
    }

    string highestRated(string cuisine) {
        auto &q = cs[cuisine];
        while (-q.top().first != fs[q.top().second].first) // 堆顶的食物评分不等于其实际值
            q.pop();
        return q.top().second;
    }
};

基数排序 ​

模板：164. 最大间距

cpp
int maximumGap(vector<int>& nums) {
    int n = nums.size();
    if (n < 2) return 0;
    vector<int> tmp(n);
    int mx = *max_element(nums.begin(), nums.end());
    int time = maxbit(mx); // 计算最高位数
    int d = 1;

    // 从低位到高位进行基数排序
    for (int i = 0; i < time; i++) {
        vector<int> count(10); // 桶
        // 统计每个桶中有几个数
        for (int j = 0; j < n; j++) {
            int digit = (nums[j] / d) % 10; // 计算第 i 位数
            count[digit]++;
        }
        // 前缀和计算在排序数组中的索引
        for (int j = 1; j < 10; j++) count[j] += count[j - 1];
        // 对 nums 进行排序
        for (int j = n - 1; j >= 0; j--) {
            int digit = (nums[j] / d) % 10;
            tmp[count[digit] - 1] = nums[j];
            count[digit]--;
        }
        copy(tmp.begin(), tmp.end(), nums.begin());
        d *= 10;
    }
    int res = 0;
    for (int i = 1; i < n; i++) res = max(res, nums[i] - nums[i - 1]);
    return res;
}

应用：2343. 裁剪数字后查询第 K 小的数字

cpp
class Solution {
public:
    vector<int> smallestTrimmedNumbers(vector<string>& nums, vector<vector<int>>& queries) {
        int n = nums.size(), m = nums[0].size();
        // 本质是问第 trim 轮中第 k 小值
        vector<vector<int>> v(m + 1); // v[i][j] 表示第 i 轮第 j 小的数对应下标
        for (int i = 0; i < n; i++) v[0].push_back(i);
        for (int i = 1; i <= m; i++)
        {
          vector<vector<int>> tmp(10);
          // 把第 i - 1 轮的结果，根据 nums 中右数第 i 位数，依次放入桶中
          for (int x: v[i - 1]) tmp[nums[x][m - i] - '0'].push_back(x);
          // 把每个桶的结果连接起来，成为第 i 轮的结果
          for (int j = 0; j < 10; j++) 
            for (int x: tmp[j]) v[i].push_back(x);
        }
        vector<int> res;
        for (auto& q: queries)
          res.push_back(v[q[1]][q[0] - 1]);
        return res;
    }
};

螺旋矩阵 ​

按四边界划分：

cpp
class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        vector <int> ans;
        if(matrix.empty()) return ans; //若数组为空，直接返回答案
        int u = 0; //赋值上下左右边界
        int d = matrix.size() - 1;
        int l = 0;
        int r = matrix[0].size() - 1;
        while(true)
        {
            for(int i = l; i <= r; ++i) ans.push_back(matrix[u][i]); //向右移动直到最右
            if(++ u > d) break; //重新设定上边界，若上边界大于下边界，则遍历遍历完成，下同
            for(int i = u; i <= d; ++i) ans.push_back(matrix[i][r]); //向下
            if(-- r < l) break; //重新设定有边界
            for(int i = r; i >= l; --i) ans.push_back(matrix[d][i]); //向左
            if(-- d < u) break; //重新设定下边界
            for(int i = d; i >= u; --i) ans.push_back(matrix[i][l]); //向上
            if(++ l > r) break; //重新设定左边界
        }
        return ans;
    }
};

按方向划分：

cpp
class Solution {
public:
    vector<vector<int>> spiralMatrix(int m, int n, ListNode* p) {
        vector<vector<int>> res(m, vector<int>(n, -1));
        int x = 0, y = 0, d = 1;
        for (int i = 0; i < m * n && p; i++)
        {
            res[x][y] = p->val;
            int a = x + dx[d], b = y + dy[d];
            if (a < 0 || a >= m || b < 0 || b >= n || res[a][b] != -1)
            {
                d = (d + 1) % 4;
                a = x + dx[d], b = y + dy[d];
            }
            x = a, y = b;
            p = p->next;
        }
        return res;
    }
};

字符串从后往前找某个字符出现的位置 ​

利用 rfind() 函数，例题：2844. 生成特殊数字的最少操作

cpp
class Solution {
public:
    int minimumOperations(string num) {
        int n = num.length();
        auto f = [&](string tail) {
            int i = num.rfind(tail[1]);
            if (i == string::npos || i == 0) return n;
            i = num.rfind(tail[0], i - 1);
            if (i == string::npos) return n;
            return n - i - 2;
        };
        return min({n - (num.find('0') != string::npos), f("00"), f("25"), f("50"), f("75")});
    }
};

KMP ​

cpp
class Solution {
public:
  int ne[10010]; // 定义 ne 数组
    int strStr(string s, string p) {
      int m = s.size(), n = p.size();
      s = '0' + s, p = '0' + p; // 使下标从 1 开始
      // 构建 ne数组
      for (int i = 2, j = 0; i <= n; i++) {
        while (j && p[i] != p[j + 1]) j = ne[j];
        if (p[i] == p[j + 1]) j++;
        ne[i] = j;
      }
	  // 匹配
      for (int i = 1, j = 0; i <= m; i++) {
        while (j && s[i] != p[j + 1]) j = ne[j];
        if (s[i] == p[j + 1]) j++;
        if (j == n)  // 匹配到了一个位置
        {
            return i - n;
            // cnt ++
            j = ne[j];
        }
      }
      return -1;
    }
};

矩阵快速幂 ​

cpp
vector<vector<int>> matrix;
void newMatrix(int n, int m)
{
    matrix = vector<vector<int>>(n, vector<int>(m));
}
vector<vector<int>> newIdMatrix(int n)
{
    vector<vector<int>> a(n, vector<int>(n));
    for (int i = 0; i < n; i++) a[i][i] = 1;
    return a;
}
vector<vector<int>> mul(vector<vector<int>> &a, vector<vector<int>> &b)
{
    vector<vector<int>> c((int)a.size(), vector<int>((int)b[0].size()));
    for (int i = 0; i < a.size(); i++)
        for (int j = 0; j < b[0].size(); j++)
        {
            for (int k = 0; k < a[i].size(); k++)
                c[i][j] = (c[i][j] + (LL)a[i][k] * b[k][j]) % MOD;
            if (c[i][j] < 0) c[i][j] += MOD;
        }
    return c;
}
vector<vector<int>> qmi(vector<vector<int>> &a, LL k)
{
    vector<vector<int>> res = newIdMatrix((int)a.size());
    while (k)
    {
        if (k & 1) res = mul(res, a);
        a = mul(a, a);
        k >>= 1;
    }
    return res;
}

// 调用示例 想要获得 a ^ k
vector<vector<int>> a = {{cnt - 1, cnt}, {n - cnt, n - 1 - cnt}};
vector<vector<int>> res = qmi(a, k);

字符串哈希 ​

cpp
mt19937 rng(chrono::steady_clock::now().time_since_epoch().count());

int rnd(int x, int y) {
    return uniform_int_distribution<int>(x, y)(rng);
}

struct HashSeq {
    vector<long long> P, H;
    int MOD, BASE;

    HashSeq() {}

    HashSeq(string &s, int MOD, int BASE): MOD(MOD), BASE(BASE) {
        int n = s.size();
        P.resize(n + 1);
        P[0] = 1;
        for (int i = 1; i <= n; i++) P[i] = P[i - 1] * BASE % MOD;
        H.resize(n + 1);
        H[0] = 0;
        for (int i = 1; i <= n; i++) H[i] = (H[i - 1] * BASE + (s[i - 1] ^ 7)) % MOD;
    }

    long long query(int l, int r) {
        return (H[r] - H[l - 1] * P[r - l + 1] % MOD + MOD) % MOD;
    }
};

int MOD1 = 998244353 + rnd(0, 1e9), BASE1 = 233 + rnd(0, 1e3);
int MOD2 = 998244353 + rnd(0, 1e9), BASE2 = 233 + rnd(0, 1e3);

struct HashString {
    HashSeq hs1, hs2;

    HashString(string &s): hs1(HashSeq(s, MOD1, BASE1)), hs2(HashSeq(s, MOD2, BASE2)) {}

    long long query(int l, int r) {
        return hs1.query(l, r) * MOD1 + hs2.query(l, r);
    }
};

双向链表插入 ​

cpp
void push_front(Node *x)
{
    x->pre = dummy;
    x->nxt = dummy->nxt;
    x->pre->nxt = x;
    x->nxt->pre = x;
}

最长公共子序列 ​

cpp
class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
      int m = text1.length(), n = text2.length();
        vector<vector<int>> dp(m + 1, vector<int>(n + 1));
        for (int i = 1; i <= m; i++) {
            char c1 = text1.at(i - 1);
            for (int j = 1; j <= n; j++) {
                char c2 = text2.at(j - 1);
                if (c1 == c2) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[m][n];

    }
};

满足下标 满足 f(i, j) 元素满足 g(nums[i], nums[j]) 的这一类题（合法范围内的可能值） ​

比如

  • abs(i - j) >= indexDifference 且
  • abs(nums[i] - nums[j]) >= valueDifference

先看 [i, j] 怎么处理：

  • 有序列表的查找
cpp
class Solution {
public:
    vector<int> findIndices(vector<int>& nums, int x, int y) {
        map<int, int> m//有序哈希表，按照值排序(方便使用二分快速查找)
        for (int j = 0; j < nums.size(); j++) {
            if (j - x >= 0) m[nums[j - x]] = j - x;
            auto it = m.lower_bound(nums[j] + y);//只需要找到一个大于等于nums[i] - y的存储在哈希表中的nums[j]
            if (it != m.end()) return {it->second, j};
            it = m.upper_bound(nums[j] - y);
            if (it != m.begin()) return {(--it)->second, j};// 只需要找到一个小于等于nums[i] - y的存储在哈希表中的nums[j], 因为upper_bound是在大于nums[j] - y的一个数，所以需要--it
        }
        return {-1, -1};
    }
};
  • 只需要找到一组下标对的情况下，可以采用贪心+枚举的方法
cpp
class Solution {
public:
    vector<int> findIndices(vector<int>& nums, int indexDifference, int valueDifference) {
        int n = nums.size();
        // mn 是满足 0 <= j <= i - indexDifference，且 nums[j] 最小的下标
        // mx 是满足 0 <= j <= i - indexDifference，且 nums[j] 最大的下标
        int mn = 0, mx = 0;
        for (int i = indexDifference; i < n; i++) {
            // 检查下标 mn 和 mx 是否满足 valueDifference
            if (abs(nums[i] - nums[mn]) >= valueDifference) return {mn, i};
            if (abs(nums[i] - nums[mx]) >= valueDifference) return {mx, i};
            int nxt = i - indexDifference + 1;
            if (nxt < n) {
                // i 要变成 i + 1 了
                // 用下标 i - indexDifference + 1 更新 mn 和 mx
                if (nums[mn] > nums[nxt]) mn = nxt;
                if (nums[mx] < nums[nxt]) mx = nxt;
            }
        }
        return {-1, -1};
    }
};

再比如：

请你找到两个下标 i 和 j ，满足 abs(i - j) >= x 且 abs(nums[i] - nums[j]) 的值最小。返回一个整数，表示下标距离至少为 x 的两个元素之间的差值绝对值的 最小值 。

  • 因为要维护最值，所以用平衡树维护
cpp
class Solution {
public:
    int minAbsoluteDifference(vector<int> &nums, int x) {
        int ans = INT_MAX, n = nums.size();
        set<int> s = {INT_MIN / 2, INT_MAX}; // 哨兵
        for (int i = x; i < n; i++) {
            s.insert(nums[i - x]);
            int y = nums[i];
            auto it = s.lower_bound(y); // 注意用 set 自带的 lower_bound，具体见视频中的解析
            ans = min(ans, min(*it - y, y - *prev(it))); // 注意不能写 *--it，这是未定义行为：万一先执行了 --it，前面的 *it-y 就错了
        }
        return ans;
    }
};

计算有序数组左右点对距离和的公式 ​

x[1]-x[0]

x[2]-x[1] x[2]-x[0]

...

x[n-1]-x[n-2] x[n-1]-x[n-3] ... x[n-1]-x[0]

通过统计每个项出现为正和为负的次数，得到下列公式

记得加 LL

res = (res + (n - 1 - 2 * i) * ((LL)a[n - 1 - i] - a[i])) % MOD;

如何判定 i * i 是否能够分割成多个整数，使其累加值为 i ？ ​

简单做法是递归，每次从当前值的低位开始截取，通过「取余」和「地板除」操作，得到截取部分和剩余部分，再继续递归处理

cpp
bool check(int t, int x) {
    if (t == x) return true;
    int d = 10;
    while (t >= d && t % d <= x) {
        if (check(t / d, x - (t % d))) return true;
        d *= 10;
    }
    return false;
}

两个互质的数相互组合，不能组成的最大整数是 a * b - a - b ​

用 的地砖铺 的地板，因为不能组成的最大整数是 ，所以只要 是 6 的倍数，且 ， 就是合法的

树形 DP 求树的直径 ​

树上任意两节点之间最长的简单路径即为树的「直径」。

我们记录当 1 为树的根时，每个节点作为子树的根向下，所能延伸的最长路径长度 d1 与次长路径（与最长路径无公共边）长度 d2，那么直径就是对于每一个点，该点 d1+d2 能取到的值中的最大值。

树形 DP 可以在存在负权边的情况下求解出树的直径。

cpp
LL d1[N], d2[N], d;

void dfs(int u, int fa)
{
    d1[u] = d2[u] = 0;
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (j == fa) continue;
        dfs(j, u);
        LL t = d1[j] + w[i]; // 无权时 d1[j] + 1
        if (t > d1[u]) d2[u] = d1[u], d1[u] = t;
        else if (t > d2[u]) d2[u] = t;
    }
    d = max(d, d1[u] + d2[u]);
}

求解树的直径的基于 DFS 的算法：

  1. 从图中任意点 s 出发跑 dfs，记录最远的点 u
  2. 从 u 开始跑 dfs，最远的点是 v，则 d(u, v) 就是直径

证明参考 https://oi.wiki/graph/tree-diameter/

写树形 DP 时初始化的注意点 ​

假如 dp 数组初始化为 -1，然后利用 f[i] == -1 来判断是否被计算过时要注意一个细节，那就是如果子树返回值小于 -1 的时候，利用取 max 来更新 f[i] 会导致更新完还是 f[i] 还是等于 -1，就没有起到区分是否计算过的作用。

正确做法是在计算一个新的状态时，如果根据题意该状态的值不可能是 -1 时，则在 dfs 开始时令 f[i]=0 表示已经计算过

用堆解决一些无向图中最小值/最小序问题 ​

如通关，CF1106D，题意都是先从无向图的根节点出发，每步去访问没访问过的节点，这个访问可能要满足一定条件（比如边权，当前权和）才能进行，问最终能访问的点/最值/字典序最小的访问序列。

想象它是一个像并查集那样逐步扩大集合的过程，每一步从当前集合中任意点出发，尝试更新一个最小的节点，那么这个过程就可以用最小堆来模拟

绝对值式子展开 ​

长度相等两数组，求 |arr1[i] - arr1[j]| + |arr2[i] - arr2[j]| + |i - j| 最大值

Use the idea that abs(A) + abs(B) = max(A+B, A-B, -A+B, -A-B).

|arr1[i] - arr1[j]| + |arr2[i] - arr2[j]| + |i - j|
 
 =  (arr1[i] + arr2[i] + i) - (arr1[j] + arr2[j] + j)
 =  (arr1[i] + arr2[i] - i) - (arr1[j] + arr2[j] - j)
 =  (arr1[i] - arr2[i] + i) - (arr1[j] - arr2[j] + j)
 =  (arr1[i] - arr2[i] - i) - (arr1[j] - arr2[j] - j)
 = -(arr1[i] + arr2[i] + i) + (arr1[j] + arr2[j] + j)
 = -(arr1[i] + arr2[i] - i) + (arr1[j] + arr2[j] - j)
 = -(arr1[i] - arr2[i] + i) + (arr1[j] - arr2[j] + j)
 = -(arr1[i] - arr2[i] - i) + (arr1[j] - arr2[j] - j)
 
因为存在四组两两等价的展开，所以可以优化为四个表达式：
A = arr1[i] + arr2[i] + i
B = arr1[i] + arr2[i] - i
C = arr1[i] - arr2[i] + i
D = arr1[i] - arr2[i] - i

max( |arr1[i] - arr1[j]| + |arr2[i] - arr2[j]| + |i - j|)
= max(max(A) - min(A),
      max(B) - min(B),
      max(C) - min(C),
      max(D) - min(D))

学会展开，然后一次遍历，维护最值即可

栈模拟思想 ​

套路：从前往后遍历 + 需要考虑相邻元素 + 有消除操作 = 栈。

用一个变量模拟栈的奇偶性即可

选定不重叠区间使得收益最大 dp+二分/哈希 ​

dp+二分的思路很熟悉了：区间按右端点排，然后遍历，选或不选的思路

哈希的思路是，当区间值域不大时，直接开哈希表或者桶，把同一结束时间的区间都放进去，遍历到 i 的时候直接看 i 这个桶就可以了，复杂度是

LL * LL ​

cpp
LL mul(LL a, LL b, LL p)
{
    LL ret=0;
    while(b)
    {
        if(b&1) ret=(ret+a)%p;
        b>>=1;a<<=1;
    }
    return ret;
}

二维前缀和与差分 ​

看这个就可以了

cpp
class Solution {
public:
    bool possibleToStamp(vector<vector<int>> &grid, int stampHeight, int stampWidth) {
        int m = grid.size(), n = grid[0].size();

        // 1. 计算 grid 的二维前缀和
        vector<vector<int>> s(m + 1, vector<int>(n + 1));
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                s[i + 1][j + 1] = s[i + 1][j] + s[i][j + 1] - s[i][j] + grid[i][j];
            }
        }

        // 2. 计算二维差分
        // 为方便第 3 步的计算，在 d 数组的最上面和最左边各加了一行（列），所以下标要 +1
        vector<vector<int>> d(m + 2, vector<int>(n + 2));
        for (int i2 = stampHeight; i2 <= m; i2++) {
            for (int j2 = stampWidth; j2 <= n; j2++) {
                int i1 = i2 - stampHeight + 1;
                int j1 = j2 - stampWidth + 1;
                if (s[i2][j2] - s[i2][j1 - 1] - s[i1 - 1][j2] + s[i1 - 1][j1 - 1] == 0) {
                    d[i1][j1]++;
                    d[i1][j2 + 1]--;
                    d[i2 + 1][j1]--;
                    d[i2 + 1][j2 + 1]++;
                }
            }
        }

        // 3. 还原二维差分矩阵对应的计数矩阵（原地计算）
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                d[i + 1][j + 1] += d[i + 1][j] + d[i][j + 1] - d[i][j];
                if (grid[i][j] == 0 && d[i + 1][j + 1] == 0) {
                    return false;
                }
            }
        }
        return true;
    }
};

预处理 1e9 以内的回文数 ​

cpp
bool inited = false;
vector<int> good;

void init() {
    if (inited) return;
    inited = true;

    for (int i = 1; i < 10; i++) good.push_back(i);

    // 首先枚举回文数一半的长度 len，以及这一半数值的上限 p
    for (int p = 10, len = 1; p <= 1e4; p *= 10, len++) {
        // 枚举回文数的一半具体是什么数
        for (int i = 1; i < p; i++) if (i % 10 != 0) {
            // 把每个数位拆开来
            vector<int> vec;
            for (int x = i, j = len; j > 0; x /= 10, j--) vec.push_back(x % 10);
            
            // 回文数长度是偶数的情况
            int v = 0;
            for (int j = 0; j < len; j++) v = v * 10 + vec[j];
            for (int j = len - 1; j >= 0; j--) v = v * 10 + vec[j];
            good.push_back(v);

            // 回文数长度是奇数的情况，需要枚举中间那一位是什么数
            for (int k = 0; k < 10; k++) {
                v = 0;
                for (int j = 0; j < len; j++) v = v * 10 + vec[j];
                v = v * 10 + k;
                for (int j = len - 1; j >= 0; j--) v = v * 10 + vec[j];
                good.push_back(v);
            }
        }
    }

    sort(good.begin(), good.end());
}

使 x 变为 y 的最小操作次数 ​

给定一些操作： 自增、自减、或者除以某个数 ，问变成 最小的操作次数

思路是贪心+记忆化搜索， 的过程中，要么纯自减，要么先变为最接近的 的倍数，然后执行除操作

每次转换为 、

记忆化搜索的复杂度为 ，是很小的

例题：

10033. 使 X 和 Y 相等的最少操作次数

LCP 20. 快速公交

判环 ​

对于有向图判断环路很简单，拓扑排序即可

cpp
bool topsort() {
	int hh = 0, tt = -1;
	for (int i = 1; i <= n; i++)
		if (!d[i])
			q[++tt] = i;
	while (hh <= tt) {
		int t = q[hh++];
		for (int i = h[t]; i != -1; i = ne[i]) {
			int j = e[i];
			d[j]--;
			if (d[j] == 0)
				q[++tt] = j;
		}
	}
	return tt == n - 1;
}

对于无向图，我想知道无环联通块的个数，怎么算呢？可以利用 dfs 求点的个数的边的个数，然后用 来判断

cpp
void dfs(int u)
{
    st[u] = 1;
    V ++;
    E += g[u].size();
    for (int v: g[u])
        if (!st[v]) dfs(v);
}

日期问题 ​

例题：输入两个日期 YYYYMMDD，返回相隔天数

代码中包含：

  • 日期问题必默模板
  • 格式化输入字符串
cpp
// 必背
const int months[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};

int is_leap(int year) {
    if (year % 4 == 0 && year % 100 || year % 400 == 0) return 1;
    return 0;
}

int get_days(int y, int m) {
    if (m == 2) return 28 + is_leap(y);
    return months[m];
}

// 本题计算
int calc(int y, int m, int d) {
    int res = 0;
    for (int i = 1; i < y; i++) res += 365 + is_leap(i);
    for (int i = 1; i < m; i++) res += get_days(y, i);
    return res + d;
}

int main() {
    int y1, m1, d1, y2, m2, d2;
    while (~scanf("%04d%02d%02d\n%04d%02d%02d", &y1, &m1, &d1, &y2, &m2, &d2))
        printf("%d\n", abs(calc(y2, m2, d2) - calc(y1, m1, d1)) + 1);
    return 0;
}

附 python 库代码

python
import datetime
def solve(t1, t2):
    t1 = datetime.date(int(t1[:4]), int(t1[4:6]), int(t1[6:]))
    t2 = datetime.date(int(t2[:4]), int(t2[4:6]), int(t2[6:]))
    if t1 > t2: t1, t2 = t2, t1
    deta = t2 - t1
    print(deta.days + 1)

[1, 2^n-1] 中每个二进制位共有多少个 1？ ​

一共 个二进制位，固定一位填 ，其余任意，发现其实所有二进制位 的个数都是

字典序问题 ​

如何自定义 cmp？

cpp
return s1 + s2 < s2 + s1; // string 数组 按字典序从小到大排序

数组元素两两分组求最大组数 ​

这类问题不知道该归纳为什么类型比较好。一个数组，两个元素作为一组，要求每组内的元素不同，例如 [1,1,2,3] 可以分为 [1,2] 和 [1,3]。分析的核心在于出现次数最多的元素出现了 d 次，若 d<=n-d，则可以分 n/2 个组；否则只能分 (n-d)*2 个组。为什么呢？想象我们有两行，a[0][0] 和 a[1][0] 就是一组，以此类推。那么我们可以把出现次数最多的元素先依次排在第一行，剩下的元素排在第二行，这样必定满足同一组的元素不同。可以用反证法证明没有更优的摆法。所以需要讨论 n 和 n-d 的关系，假如某个元素出现次数超过一半，多出来的部分肯定不能配对的

例题在 你可以工作的最大周数，使数组中所有元素相等的最小开销

数组 a 和 b 有多少对下标 a[i] 整除 b[j] ​

方法一是朴素枚举 的因子，复杂度是

cpp
for (int x : nums1) {
    for (int d = 1; d * d <= x; d++) {
        if (x % d) {
            continue;
        }
        cnt[d]++;
        if (d * d < x) { // 注意这里的细节
            cnt[x / d]++;
        }
    }
}

方法二：以 为主视角，寻找在 中的倍数

cpp
long long ans = 0;
int m = ranges::max_element(cnt1)->first; // 先求出 U
for (auto& [i, c] : cnt2) { // b 数组的数字事先存哈希表
    int s = 0;
    for (int j = i; j <= m; j += i) { // 枚举倍数
        s += cnt1.contains(j) ? cnt1[j] : 0;
    }
    ans += (long long) s * c;
}

这个方法的复杂度是多少呢？由于哈希表每个数出现一次，考虑调和级数 就是 ，复杂度比方法一小

矩阵对角线元素的特点 ​

https://pic.leetcode-cn.com/b4425d9def38f3f74a99525dd2cbe2b5257531f307231294dede11eec729f6cf-聚合键.PNG

左下到右上的：i+j 是定值

左上到右下的：i-j 是定值

位运算，gcd 子数组通用模板 ​

  • 求出所有子数组的按位或的结果，以及值等于该结果的子数组的个数
  • 求按位或结果等于任意给定数字的子数组的最短长度/最长长度

可用于 and、or、gcd、lcm

特点：固定右端点，结果具有单调性质，相同结果的左端点会形成一段连续区间

cpp
        map<int, LL> res; // 统计子数组数量
        vector<array<int, 3>> a; // 左端点闭区间 [a[0], a[1]] 值为 a[2]
        for (int i = 0; i < nums.size(); i++) {
            int cur = nums[i];
            for (auto &v: a) {
                v[2] |= cur; // 给定运算
            }
            a.push_back({i, i, cur});
            int p = 0; // 原地去重
            for (int i = 1; i < a.size(); i++) {
                if (a[p][2] != a[i][2]) {
                    p ++;
                    a[p] = a[i];
                } else {
                    a[p][1] = a[i][1];
                }
            }
            a.resize(p + 1);
            // 这里求的是大于等于 k 的最短子数组长度
            for (auto &t: a) {
                if (t[2] >= k) {
                    ans = min(ans, i - t[1] + 1); 
                }
            }
            // 累加子数组
            for (auto &t: a) {
                res[t[2]] += t[1] - t[0] + 1;
            }
        }

另一个模板是枚举 种 and、or 值，找到每个二进制位不同的最近位置

cpp
class Solution {
public:
    long long countSubarrays(vector<int>& nums, int K) {
        int n = nums.size();
        const int MAXP = 30;

        // last[i][p]：在位置 i 的左边（含位置 i），二进制第 p 位是 0 的最近位置在哪
        int last[n][MAXP];
        for (int j = 0; j < MAXP; j++) {
            if (nums[0] >> j & 1) last[0][j] = -1;
            else last[0][j] = 0;
        }
        for (int i = 1; i < n; i++) for (int j = 0; j < MAXP; j++) {
            last[i][j] = last[i - 1][j];
            if (nums[i] >> j & 1 ^ 1) last[i][j] = i;
        }

        long long ans = 0;
        // 枚举子数组右端点
        for (int i = 0; i < n; i++) {
            // 对于二进制的每一位，拿出上一个 0 在什么位置
            vector<int> pos;
            for (int j = 0; j < MAXP; j++) if (last[i][j] >= 0) pos.push_back(last[i][j]);
            sort(pos.begin(), pos.end());
            pos.resize(unique(pos.begin(), pos.end()) - pos.begin());
            reverse(pos.begin(), pos.end());
            // 枚举 logX 种 AND 值
            int v = nums[i];
            for (int j = 0; j < pos.size(); j++) {
                v &= nums[pos[j]];
                if (v < K) break;
                if (v == K) {
                    // 发现了目标值，求一下这一段子数组的长度
                    if (j + 1 == pos.size()) ans += pos[j] + 1;
                    else ans += pos[j] - pos[j + 1];
                }
            }
        }
        return ans;
    }
};

因为具有单调性，还可以考虑滑窗来做，但是运算不具有可逆性的时候，需要用到一个栈来维护信息

例题见 3171. 找到按位或最接近 K 的子数组 这篇题解

cpp
class Solution {
public:
    int minimumDifference(vector<int>& nums, int k) {
        int ans = INT_MAX, left = 0, bottom = 0, right_or = 0;
        for (int right = 0; right < nums.size(); right++) {
            right_or |= nums[right];
            while (left <= right && (nums[left] | right_or) > k) {
                ans = min(ans, (nums[left] | right_or) - k);
                left++;
                if (bottom < left) {
                    // 重新构建一个栈
                    for (int i = right - 1; i >= left; i--) {
                        nums[i] |= nums[i + 1];
                    }
                    bottom = right;
                    right_or = 0;
                }
            }
            if (left <= right) {
                ans = min(ans, k - (nums[left] | right_or));
            }
        }
        return ans;
    }
};

a 是子串，b 是子序列 ​

有一个原串不知道，给两个字符串，满足上述条件，问原串的最小长度。转化为 b 中某一段 cover 了 a，相当于找到 a 的最长子序列，是 b 的子串，然后加上 b 剩下的就是最小长度

cpp
        cin >> a >> b;
        // a 是子串 b 是子序列
        // a 的子序列是 b 的子串
        int res = 0;
        for (int i = 0; i < b.size(); i++) {
            int k = i;
            for (int j = 0; j < a.size(); j++) {
                if (b[k] == a[j]) {
                    k ++;
                }
            }
            res = max(res, k - i);
        }
        cout << b.size() - res + a.size() << endl;

分配 1 和 -1 使得最大化最小值 ​

有 ， 两个数，每轮给 ，（只可能是 ，，），选择让 或者 ，使得最后 ， 的最小值最大。首先如果 ， 不同，肯定是谁大就加谁，对于 和 ，先把它们的次数存起来。最后通过二分判断是否能达到某个值，这样判断是最简单好懂的

cpp
        auto check = [](int A, int B, int C, int D, int t) -> bool {
            if (A < t) {
                C -= t - A;
                A = t;
            }
            if (B < t) {
                C -= t - B;
                B = t;
            }
            // C 是待分配的加的量 D 是待分配的减的量
            if (C < 0) {
                return false;
            }
            int r = A - t + B - t;
            return r + C >= D;
        };

判断 [l,r] 是否互不相同 ​

记录每个 a[i] 最近的左侧出现位置 left[i]，维护 left[i] 的前缀最大值，只要判断 mx[r] 是否小于 l 即可

每次操作任意子数组，使得全相等/A变B 的最小次数 ​

类型一

给你一个长度为 n 的整数数组，每次操作将会使 n - 1 个元素增加 1 。返回让数组所有元素相等的最小操作次数。

逆向思维，n-1 个数 +1 相当于 1 个数 -1，所以转化为把每个数变为数组最小值的操作数即可

类型二

每次选择子数组，元素 +1，使得 nums 变为 target 的最小操作数

考虑每个数对答案的贡献，累加相邻元素差值中大于 0 的部分

严谨证明见题解

类型三

每次选择子数组，元素 +1 或 -1，使得 nums 变为 target 的最小操作数

先把两数组的差值数组求出来，目标是使其元素全部变成 0

原地求差值数组的差分数组，考虑每个操作

  • 要么使某项 +1，另一项 -1
  • 要么使某项自己 +1 或 -1

这就转化为求差分数组中正数和与负数和的绝对值的较大者，即为答案（转化思路是，正和负先两两配对抵消，剩下的自己消化）

补全排列：找环 ​

补全排列 C，其中 C[i] 要么是 A[i] 要么是 B[i]，其中 A、B 也是排列，问方案数

基于排列的性质，假设某个位置确定，其余位置也一并确定，例如下面的例子

1 4 2 3
4 3 1 2

第一个位置选 1 或 4 会决定后面的选择，这些依赖关系会形成一个环。处理上，用并查集将环上的数字合并（即 A[i] 和 B[i]）会好写很多

cpp
for (int i = 1, x; i <= n; i++) {
    cin >> x;
    if (x == 0 && a[i] != b[i]) {
        int dx = find(a[i]), dy = find(b[i]);
        if (dx == dy) { // 表示遇到了环上最后一部分，统计答案
            res = res * 2 % MOD;
        } else {
            p[dx] = dy; // 合并
        }
    }
}

寻找 j 使得 dis(1,j)+dis(i,j) 最小 ​

这是经典的分层图的套路

  • 对于 可在原图完成， 可在反图中求 完成，如何统一起来？
  • 假设 是原图的点，反图的点设为 ，建立 的边权为 的边，就有 了，用 求解最短路即可
  • 例题见 CF1725M

通过 floor 把 a 变成 b ​

给定 和 ，每次操作选定任意 ，令 ，，问最少几次操作可以使 ？

关键在于转化为最小化操作后 的值，然后分 的奇偶性来讨论，由下取整的性质，不难发现 要么取 ，要么取

题源 CF1901C题解区

数组分若干段，最大化 sigma(i*S[i]) ​

给数组，可以分任意段，假设分了 段，求 的最大值，其中 是这一段的元素和

本质：切分一段后，后缀和的贡献多一倍！得到一个贪心的思路是：从后往前遍历，只要当前的 sum[i:n] > 0 就可以切一刀

矩阵顺时针旋转 90° ​

空间写法

cpp
// 顺时针旋转矩阵 90°
vector<vector<int>> rotate(vector<vector<int>>& a) {
    int m = a.size();
    int n = a[0].size();
    vector<vector<int>> b(n, vector<int>(m));
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            b[j][m - 1 - i] = a[i][j];
        }
    }
    return b;
}

如果是方阵的话，可以做到 空间，思路是转置+每一行翻转

cpp
void rotate(vector<vector<int>>& matrix) {
    int n = matrix.size();
    // 水平翻转
    for (int i = 0; i < n / 2; ++i) {
        for (int j = 0; j < n; ++j) {
            swap(matrix[i][j], matrix[n - i - 1][j]);
        }
    }
    // 主对角线翻转
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < i; ++j) {
            swap(matrix[i][j], matrix[j][i]);
        }
    }
}

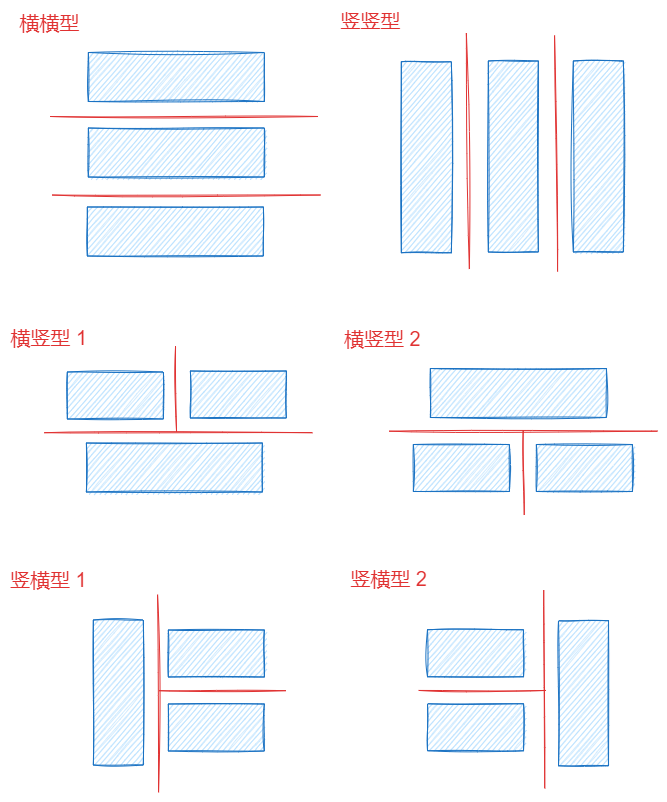
矩阵分成三个部分，共有 6 种情况 ​

如图，学会分类讨论

题目链接

最长路转化为最短路 ​

最常见的是边权取反

如果又有正又有负怎么办？增加势能法/构造等价方案法，使得全部边权都非负，把边增加一个值，最后再减回这个量即可

三指针滑窗 ​

如果要求窗口内恰有 个元素，可以转化为至少有 个减去至少 个，也可以直接三指针滑窗，用 l1 和 l2 分别维护即可，例题3306. 元音辅音字符串计数 II

c++
const int mask = 1065233;
class Solution {
public:
    using LL = long long;
    long long countOfSubstrings(string word, int k) {
        LL res = 0;
        int cnt1[26]{}, cnt2[26]{};
        int sz_v1 = 0, sz_v2 = 0;
        int cnt_c1 = 0, cnt_c2 = 0;
        int l1 = 0, l2 = 0;
        for (int c: word) {
            c -= 'a';
            if (mask >> c & 1) {
                if (cnt1[c] ++ == 0) {
                    sz_v1 ++;
                }
                if (cnt2[c] ++ == 0) {
                    sz_v2 ++;
                }
            } else {
                cnt_c1 ++;
                cnt_c2 ++;
            }
            
            while (sz_v1 == 5 && cnt_c1 >= k) {
                int out = word[l1] - 'a';
                if (mask >> out & 1) {
                    if (-- cnt1[out] == 0) {
                        sz_v1 --;
                    }
                } else {
                    cnt_c1 --;
                }
                l1 ++;
            }
            
            while (sz_v2 == 5 && cnt_c2 > k) {
                int out = word[l2] - 'a';
                if (mask >> out & 1) {
                    if (-- cnt2[out] == 0) {
                        sz_v2 --;
                    }
                } else {
                    cnt_c2 --;
                }
                l2 ++;
            }
            
            res += l1 - l2;
        }
        return res;
    }
};

给定若干差分区间，选择最少区间得到目标数组 ​

贪心思路：从左到右遍历下标，如果当前差分值小于目标，就需要选出一些区间来覆盖当前点

怎么选？用一个最大堆，存下所有左端点不超过 的区间的右端点，每次贪心地选择最大的右端点

原题见 LC3362

Updated at:

If you have any advice, please leave a message:)

Copyright@ 2024 Ricky Daxia