小感想
- 比如常规定义
f[i][j]表示第i个物品放第j个位置的最大值,其实有一种复杂度更低的定义方式,f[i][j]表示第i个物品放不放在j的最大值,转移时就两种情况,放->f[i-1][j-1],不放->f[i][j-1] - 一道题缝了完全背包跟多重背包的话,根据容量分开计算(它们的枚举顺序都不同)
- 环形石子合并,变成
2n的链,用记忆化搜索求一遍,最后遍历f[i][i+n-1]求最值 - 区间 DP,确定操作顺序,一个区间操作完的最优情况一定是最后一个操作边界,假如是中间的话,在从一个边界到另一个边界的过程中可以顺手操作中间这个,没必要留到最后
- 看到图论相关的 DP,想想这个图是有向图还是无向图?可能存在环吗?存在环的话要不要缩点?边的指向关系是谁指向谁
- 环形处理见 P1357 花园
- 建图技巧:题目说要在矩阵或数组的单元格中跳跃,从值小的跳到大的,显然是有向无环图最长路。第一点:同一行/列,只在大小相邻的点之间建边,即
u<v<w,建(u,v)和(v,w)。第二点:对于同值节点组成的集合,设S、T,建立dummy节点,建(S, dummy)和(dummy, T),这样就把边数由|S||T|降为|S|+|T| - 关于序列(字符串) DP,需要遍历窗口的状态,可以考虑用状压表示窗口的状态
- 序列 DP ,对相邻位置有要求时,处理当前状态不一定要和全部前置状态比较,只需要记录前置状态中 DP 的最大值和次大值对应的状态即可
- 下标为负时怎么处理、char 转 int 以便处理:见 3320. 统计能获胜的出招序列数 的代码
- 数组中选两个不相交的子集,可以设计状态为
f[i][j][k]表示前i个数,第一个子序列的状态为j,第二个子序列的状态为k的方案数,然后考虑第i个数:不放、放第一个、放第二个的转移 - 给一个由
a、b、c构成的字符串,使得字符串不含abc子序列最少删除多少个字符?这个问题可以用状态机来思考,f[i][0/1/2]表示 没有a,有a没有ab 和 有ab没有abc,答案为min(f[n])- 进阶:如果每次修改一个字符,如何快速求出每次修改后的答案?单点修改->线段树,维护 a:区间有多少个 a。b:区间有多少个 b。c:区间有多少个 c。ab:要使区间没有子序列 ab,至少要操作多少次。bc:要使区间没有子序列 bc,至少要操作多少次。abc:要使区间没有子序列 abc,至少要操作多少次。 例题为 CF1609E
- 粉刷房子变形题:除了相邻房子颜色不相等,还要求对称位置颜色不相等(即 )。加上这个限制之后怎么做?改变枚举顺序,按照 这样的顺序枚举,这样第 个与第 个相邻,且 为奇数时, 与 颜色不能相等。因此维护 表示第 个颜色为 ,第 个颜色为 的集合即可。这里的初始化是 ,然后从 开始枚举。题目见 LC3429
- 树形 DP 题,包含反转子树权值操作的话,就要考虑维护子树的最大和以及最小和。如果题目中还限制翻转一个点后,往下 级儿子才可以翻转,就要多设计一个状态表示「最近翻转祖先的距离」或者「当前还需往下多少步才可以翻转」。如果维护的状态表示「距离至少为 」,那么计算答案时要取后缀最值。例题参考 LC3544
- 划分型 DP 中,需要保证子数组的极差不超过 ,枚举右端点时,怎么确定左端点呢?方法一: 用一个
multiset维护区间内的元素,只要*prev(s.end())-*s.begin()>k就移动左端点。方法二: 用单调队列维护滑动窗口的最值,此法的复杂度更优
刷表法
以「树形 DP + 状态压缩」为例:在树形 DP 中,一种做法是 DFS 返回一个数组,表示子树对应的 DP 信息。在得到所有子树 DP 信息后,枚举所有状态,套用转移方程更新当前节点的 DP 信息
这种做法比较慢,有两个优化的点
- 每次 DFS 完一个子树,就用子树的 DP 信息更新当前节点的 DP 信息(将「枚举」变为「合并」)
- DFS 返回值定义为哈希表,相比数组可以避免遍历很多无效状态
状态设计
Two out of three
给定一个数组,每次从前三个数中选两个数删除,代价是较大的元素值。问全部删除的最小代价
这题需要先观察出一个性质:每次操作的时候,剩下的数的下标一定是 ,这个性质可以通过归纳法证明
借助这个性质可以设计 表示剩余的最左边下标为 和 时的最小代价,此时就是从 中选两个数删,然后转移到对应的状态。初始值为
由于是从 转移到 ,因此 DP 数组需要开大一些,最后判断答案的时候判断大于 的下标即可
for (int i = 0; i < n; i++) {
for (int j = i + 1; j <= n; j++) {
f[j + 1][j + 2] = min(f[j + 1][j + 2], f[i][j] + max(nums[i], nums[j]));
f[j][j + 2] = min(f[j][j + 2], f[i][j] + max(nums[i], nums[j + 1]));
f[i][j + 2] = min(f[i][j + 2], f[i][j] + max(nums[j], nums[j + 1]));
}
}
int res = 0x3f3f3f3f;
for (int i = n; i < n + 3; i++) {
for (int j = n; j < n + 3; j++) {
res = min(res, f[i][j]);
}
}进阶:记录方案数,代码很好理解
auto dfs = [&](auto &&dfs, int i, int j) -> int {
if (j >= n) {
return a[i];
} else if (j == n - 1) {
return max(a[i], a[j]);
}
if (f[i][j] > 0) {
return f[i][j];
}
int x = dfs(dfs, j + 1, j + 2) + max(a[i], a[j]);
int y = dfs(dfs, j, j + 2) + max(a[i], a[j + 1]);
int z = dfs(dfs, i, j + 2) + max(a[j], a[j + 1]);
f[i][j] = min(x, min(y, z));
return f[i][j];
};
auto output = [&](auto &&output, int i, int j) -> void {
if (j >= n) {
cout << i + 1 << '\n';
return;
} else if (j == n - 1) {
cout << i + 1 << ' ' << j + 1 << '\n';
return;
}
int x = dfs(dfs, j + 1, j + 2) + max(a[i], a[j]);
int y = dfs(dfs, j, j + 2) + max(a[i], a[j + 1]);
int z = dfs(dfs, i, j + 2) + max(a[j], a[j + 1]);
int mn = min(x, min(y, z));
if (x == mn) {
cout << i + 1 << ' ' << j + 1 << '\n';
output(output, j + 1, j + 2);
} else if (y == mn) {
cout << i + 1 << ' ' << j + 1 + 1 << '\n';
output(output, j, j + 2);
} else {
cout << j + 1 << ' ' << j + 1 + 1 << '\n';
output(output, i, j + 2);
}
};求 1 号点到 n 号点长度不超过 d[n]+K 的路径数
P3953 有向图,无重边和自环,存在权值为
0的边,设1->n的最短路径为d,求1->n的长度不超过d+K的路径数(可能存在无穷条,此时输出-1) 点数、边数范围是1e5,K范围是50

- 怎么判断是不是无穷?当计算状态
f[u][k]时记录st[u][k]=true,如果在此过程中又碰到计算f[u][k],那就说明答案是无穷 - 由于状态转移方程是要寻找
u->v的u,可以存一个反图,方便转移
int dp(int u, int k) {
if (k < 0) {
return 0;
}
if (st[u][k]) {
flag = true;
return 0;
}
if (f[u][k] != -1) {
return f[u][k];
}
st[u][k] = true;
int &res = f[u][k];
res = 0;
for (auto &[v, w]: g2[u]) {
res = (res + dp(v, dist[u] + k - dist[v] - w)) % P;
if (flag) {
return 0;
}
}
st[u][k] = false;
return res;
}
cin >> n >> m >> k >> P;
memset(f, -1, sizeof(f));
memset(st, 0, sizeof(st));
for (int i = 1; i <= n; i++) {
g1[i].clear();
g2[i].clear();
}
for (int i = 0; i < m; i++) {
int x, y, w;
cin >> x >> y >> w;
g1[x].push_back({y, w});
g2[y].push_back({x, w});
}
dijkstra();
dp(1, 0);
f[1][0] = 1;
int res = 0;
for (int i = 0; i <= k; i++) {
res = (res + dp(n, i)) % P;
}
if (flag) {
cout << -1 << endl;
} else {
cout << res << endl;
}
flag = false;构造数组和为 m,且元素异或和为 0 的方案数
思路:异或和为 ,意味着每个二进制位上的 出现了偶数次,枚举最低位上有 个 ,然后把当前的和 右移一位,就得到了一个子问题
定义 表示这 个数中,元素和为 的方案数。转移的时候枚举最低位上 的个数 ,得到
例题见 ARC116D
f[0] = 1;
for (int i = 2; i <= m; i += 2) {
for (int j = 0; j <= i && j <= n; j += 2) {
f[i] = (f[i] + f[(i - j) / 2] * c[j]) % mod;
}
}树上背包
选课
现在有
n门课程,第i门课程的学分为a[i],每门课程有零门或一门先修课,有先修课的课程需要先学完其先修课,才能学习该课程。 一位学生要学习m门课程,求其能获得的最多学分数。
把父节点 x 和儿子看成物品,一共 n 个物品,容量为 m,典型的 01 背包。定义 f(x, i, j) 表示以 x 为根的子树,考虑了前 i 个子树,选了 j 个物品的最大价值。f(x,i,j)<-f(x,i-1,j) 或者 f(x,i,j)<-f(x,i-1,j-v[i])+w[i]
转移方程就是:规定根节点必选(因为不选根节点就无法选子节点),枚举子节点选多少个,即 f[x][i][j]=max{f[x][i-1][j], f[x][i-1][j-k]+f[v][sz[v]][k],其中 0<=k<j,其中前者又是 k=0 时的情况,因此可合并到后面的式子中
边界条件:f[x][1][0]=0, f[x][1][1]=1,分别代表不选和选根节点。复杂度是
void dfs(int u) {
f[u][1] = s[u];
for (int v: g[u]) {
dfs(v);
for (int j = m; j > 0; j--) {
for (int k = 0; k < j; k++) {
f[u][j] = max(f[u][j], f[u][j - k] + f[v][k]);
}
}
}
}一个通过后序遍历优化为 的链接
取气球
有
n个气球用绳子连接,构成一棵树,给出点权和边权
- 要么删一条边,获得子树所有气球
- 要么删掉一个根节点,获得子树所有气球 问不超过给定代价的情况下,最多拿走几个气球
定义状态是 f[u][j] 表示以 u 为根的子树,获得 j 个气球的最小代价
边权转点权的技巧:把每个气球上方的边看成一个点,点权为 b[u],表示花 b[u] 代价获得 u 这棵子树
- 如果
b[u]<=j,直接获得子树是最优的,f[u][j]=b[u] - 对子树转移:
f[u][j+k]=min(f[u][j+k], f[u][j]+f[v][k]) - 对于
u的代价不小于a[u]的情况:f[u][sz[u]-1]=min(f[u][sz[u]-1],a[u]),f[u][sz[u]]=min(f[u][sz[u]],b[u])
下面这种写法参考 oi-wiki 的写法,使用了子树合并的方式,可以证明复杂度是 的
int dfs(int u) {
memset(f[u], 0x3f, sizeof f[u]);
f[u][0] = 0; // 获得 0 个气球
int p = 1;
for (auto &v: g[u]) {
int sz = dfs(v);
for (int i = min(p, n); i >= 0; i--) { // 当前选了 i 个点 属于第三维 倒序
for (int j = 1; j <= sz && i + j <= n; j++) { // 更新未来的答案
f[u][i + j] = min(f[u][i + j], f[u][i] + f[v][j]);
}
}
p += sz;
}
f[u][p - 1] = min(f[u][p - 1], a[u]); // 删掉根节点的代价是 a[u] 获得子树
if (u > 1) {
f[u][p] = min(f[u][p], b[u]); // 删掉根节点所连的边代价是 b[u] 获得整个子树
}
return p;
}
int res = 0;
for (int i = 1; i <= n; i++) {
if (f[1][i] <= m) {
res = i;
}
}LC 例题
题源 LC3562
给定树和每个点的买入价格和卖出价格,父节点买入,子节点可以半价买入。求不超过给定总成本,最大利润
我们需要知道子节点 在成本不超过 的情况下,最多能获得的利润。不妨直接让 DFS 返回一个数组,这样就知道每个 对应的利润来转移
auto dfs = [&](this auto&& dfs, int x) -> vector<array<int, 2>> {
// 计算从 x 的所有儿子子树 y 中,能得到的最大利润之和
vector<array<int, 2>> sub_f(budget + 1);
for (int y : g[x]) {
auto fy = dfs(y);
for (int j = budget; j >= 0; j--) {
// 枚举子树 y 的预算为 jy
// 当作一个体积为 jy,价值为 fy[jy][k] 的物品
for (int jy = 0; jy <= j; jy++) {
for (int k = 0; k < 2; k++) {
sub_f[j][k] = max(sub_f[j][k], sub_f[j - jy][k] + fy[jy][k]);
}
}
}
}
vector<array<int, 2>> f(budget + 1);
for (int j = 0; j <= budget; j++) {
for (int k = 0; k < 2; k++) {
int cost = present[x] / (k + 1);
if (j >= cost) {
// 不买 x,转移来源是 sub_f[j][0]
// 买 x,转移来源为 sub_f[j-cost][1],因为对于子树来说,父节点一定买
f[j][k] = max(sub_f[j][0], sub_f[j - cost][1] + future[x] - cost);
} else { // 只能不买 x
f[j][k] = sub_f[j][0];
}
}
}
return f;
};正常写法
auto dfs = [&](this auto &&dfs, int u) -> void {
int sub_f[budget + 1][2];
memset(sub_f, 0, sizeof(sub_f));
for (int v: g[u]) {
dfs(v);
for (int j = budget; j >= 0; j--) {
for (int i = 0; i <= j; i++) {
for (int k = 0; k < 2; k++) {
// 临时数组 合并子树的情况
sub_f[j][k] = max(sub_f[j][k], sub_f[j - i][k] + f[v][i][k]);
}
}
}
}
for (int j = 0; j <= budget; j++) {
f[u][j][0] = f[u][j][1] = sub_f[j][0]; // 不选
int cost = present[u - 1];
// 选
if (j >= cost) {
f[u][j][0] = max(f[u][j][0], sub_f[j - cost][1] + future[u - 1] - cost);
}
cost /= 2;
if (j >= cost) {
f[u][j][1] = max(f[u][j][1], sub_f[j - cost][1] + future[u - 1] - cost);
}
}
};划分型 DP
K 个不相交子数组的最大得分
x个子数组的能量值定义为strength = sum[1] * x - sum[2] * (x - 1) + sum[3] * (x - 2) - sum[4] * (x - 3) + ... + sum[x] * 1,其中sum[i]是第i个子数组的和。更正式的,能量值是满足1 <= i <= x的所有i对应的(-1)(i+1)sum[i] * (x - i + 1)之和。 你需要在nums中选择k个 不相交子数组 ,使得 能量值最大 。
本题状态定义有些不一样,因为一定要选 k 个,所以定义 f[i][j][0/1] 表示考虑前 i 个数,第 i 个数是否在第 j 段的最大得分(而不是当前有 j 段)
这样定义有什么好处呢,当知道了 a[i] 在第几段后,可以直接求出对于答案的最终贡献!
转移是很简单的:不选,选(1)和前一个数分在一起(2)单独开一段
划分段数转换为前后缀和
你可以将
nums分割成多个子数组。第i个子数组由元素nums[l..r]组成,其代价为:
(nums[0] + nums[1] + ... + nums[r] + k * i) * (cost[l] + cost[l + 1] + ... + cost[r])返回通过任何有效划分得到的 最小 总代价
数据范围是
题意转换为两部分
(nums[1] + ... + nums[r]) * (cost[l] + ... + cost[r])k * i * (cost[l] + ... + cost[r])
第一部分很简单,难点在于第二部分。参考题解中的图可以发现,划分段数跟倍率相关,转化为 cost 的某一子段和被统计的次数,进而得出本质:第二部分的代价就是 cost 的后缀和
类似的转换思路见 CF1175D
代码见 LC3500
区间 DP
翻转子段
CF1519D 输入
n(≤5000)和两个长为n的整数数组a和b,元素值均在[1,1e7]中。 你可以至多反转一次a的某个子数组,求sum(a[i]*b[i])的最大值(即最大化a[0]*b[0]+a[1]*b[1]+...+a[n-1]*b[n-1])。
用区间 DP 的思路想,设 f[i][j] 表示翻转 [i,j] 的最大和,扩展区间的转移方程很容易得到,考虑端点即可
注意初始化时,由于会用到 f[i+1][i],因此把这个状态也初始化一下
LL s = 0;
for (int i = 1; i <= n; i++)
{
cin >> b[i];
s += a[i] * b[i];
}
for (int i = 1; i <= n; i++)
f[i][i] = f[i + 1][i] = s;
for (int len = 2; len <= n; len++)
for (int i = 1; i + len - 1 <= n; i++)
{
int j = i + len - 1;
f[i][j] = f[i + 1][j - 1] - a[i] * b[i] - a[j] * b[j] + a[i] * b[j] + a[j] * b[i];
}砖块涂色
CF1114D 有
n个砖块排成一排,从左到右编号为1∼n(n <= 5000)。 其中,第i个砖块的初始颜色为ci。 我们规定,如果编号范围[i,j]内的所有砖块的颜色都相同,且当第i−1和 第j+1个砖块存在时,这两个砖块的颜色和区间[i,j]的颜色均不同, 则砖块i和j属于同一个连通块。 例如,[3,3,3]有 1 个连通块,[5,2,4,4]有 3 个连通块。 现在,要对砖块进行涂色操作。 开始所有操作之前,你需要任选一个砖块作为起始砖块。 每次操作:
- 任选一种颜色
- 将最开始选定的起始砖块所在连通块中包含的所有砖块都涂为选定颜色 请问,至少需要多少次操作,才能使所有砖块都具有同一种颜色。
定义 f[i][j][0/1] 表示染 [i,j] 这个区间,最后颜色等于 a[i] 还是 a[j] 的步数
转移的时候考虑 f[i+1][j] 和 f[i][j-1] 即可,难点在于想到最后一步染的颜色必定是等于端点的颜色
memset(f, 0x3f, sizeof f);
for (int i = 1; i <= n; i++)
{
f[i][i][0] = f[i][i][1] = 0;
f[i + 1][i][0] = f[i + 1][i][1] = 0;
}
for (int len = 2; len <= n; len++)
for (int i = 1; i + len - 1 <= n; i++)
{
int j = i + len - 1;
for (int k = 0; k <= 1; k++)
{
int t = k ? a[j] : a[i + 1];
f[i][j][0] = min(f[i][j][0], f[i + 1][j][k] + (a[i] != t));
t = k ? a[j - 1] : a[i];
f[i][j][1] = min(f[i][j][1], f[i][j - 1][k] + (a[j] != t));
}
}
cout << min(f[1][n][0], f[1][n][1]) << endl;环形数组的区间 DP
每颗珠子有头尾标记(前一个的尾标记等于后一个的头标记),合并代价为
m*r*n,假设珠子为(m,r)(r,n),合并后变为(m,n)。问环形珠子串合并的最大代价
以往的区间 dp 我们把区间 [a,b] 分为 [a,k],[k+1,b],但本题分割点 k 要作为两个区间的共同端点使用,因此是 [a,k],[k,b]。 此外,本题枚举的区间长度为 n+1,在处理上每次读入一个 a[i],我们令 a[i+n]=a[i];枚举时,窗口从 1 移到 n*2 的位置。注意,len=2 的时候只有一个球, 即 len=k 时只有 k-1 个球。 转移方程为 f[i][j] = max(f[i][j], f[i][k] + f[k][j] + a[i] * a[k] * a[j])。
for (int len = 3; len <= n + 1; len ++)
for (int i = 1; i + len - 1 <= n * 2; i++)
{
int j = i + len - 1;
for (int k = i + 1; k < j; k++)
f[i][j] = max(f[i][j], f[i][k] + f[k][j] + a[i] * a[k] * a[j]);
}
int res = 0;
for (int i = 1; i <= n; i++) res = max(res, f[i][i + n]);注意枚举顺序
你有一个凸的
n边形,其每个顶点都有一个整数值。给定一个整数数组values,其中values[i]是第i个顶点的值(即 顺时针顺序 )。 假设将多边形 剖分 为n - 2个三角形。对于每个三角形,该三角形的值是顶点标记的乘积,三角剖分的分数是进行三角剖分后所有n - 2个三角形的值之和。 返回 多边形进行三角剖分后可以得到的最低分 。
本题考虑枚举 i j 的做法:f[i][j] = f[i][k] + f[k][j] = v[i]*v[j]*v[k],其中 k ∈ [i+1,j-1]
- 由于
i小于k,因此倒序枚举i - 由于
j大于k,因此正序枚举j
class Solution {
public:
int minScoreTriangulation(vector<int>& values) {
int n = values.size();
int f[n][n];
memset(f, 0, sizeof f);
for (int l = n - 3; l >= 0; l--)
for (int r = l + 2; r < n; r++)
{
f[l][r] = INT_MAX;
for (int k = l + 1; k < r; k++)
f[l][r] = min(f[l][r], f[l][k] + f[k][r] + values[l] * values[k] * values[r]);
}
return f[0][n - 1];
}
};统计不同的回文子序列
LC730 返回不同的非空回文子序列个数,
n是1000
怎么去重?定义 f[i][j] 表示区间 [i,j] 的不同回文子序列数,如果 s[i]=s[j]=x,那么 f[i][j] 增加了 f[i-1][j+1] 中的方案两端拼 xx + 单独的 xx + 单独的 x。去重的时候考虑枚举端点字符 x,寻找 [i+1,j-1] 中有没有出现一段区间 [l,r],其中 s[l]=s[r]=x,有的话只需要减去 f[l+1][r-1] 即可。这个可以通过预处理 nxt 和 pre 数组得到。特别考虑如果 l==r 时怎么处理(单独的 x 不能算进去),以及 s[i] != s[j] 时,根据状态定义可以用容斥原理解决(f[i+1][j]+f[i][j-1]-f[i+1][j-1])
for sz := 2; sz <= n; sz++ {
for i := 0; i + sz - 1 < n; i++ {
j := i + sz - 1
if s[i] == s[j] {
low, high := nxt[i][s[i] - 'a'], pre[j][s[i] - 'a']
if low > high {
f[i][j] = (f[i + 1][j - 1] * 2 + 2) % MOD
} else if low == high {
f[i][j] = (f[i + 1][j - 1] * 2 + 1) % MOD
} else {
f[i][j] = (f[i + 1][j - 1] * 2 - f[low + 1][high - 1] + MOD) % MOD
}
} else {
f[i][j] = (f[i + 1][j] + f[i][j - 1] - f[i + 1][j - 1] + MOD) % MOD
}
}
}背包 DP
01 背包求方案数
每件物品用一次,求最优选法的方案数
维护 f[i][j] 表示前 i 个物品中选体积不超过 j 的最大价值和,同时维护 g[i][j] 表示对应最大价值和时的方案数。初始化时,g[i] 都置成 1,一开始时最大价值为 0,对应什么都不选,是一种方案
for (int i = 0; i <= m; i++) g[i] = 1;
for (int i = 1; i <= n; i++) {
cin >> v >> w;
for (int j = m; j >= v; j--) {
if (f[j] < f[j - v] + w) {
f[j] = f[j - v] + w;
g[j] = g[j - v];
} else if (f[j] == f[j - v] + w) {
g[j] = (g[j] + g[j - v]) % MOD;
}
}
}
cout << g[m] << endl;可撤销多重背包方案数
参考 这篇博客
N种物品,第i种有c[i]个,重量为v[i]。求对于j=1,2,...,M,求背包重量为j时的方案数
朴素计算是 的,注意到 f[i][j] 只会由满足 j 与 k 模 v[i] 同余的状态转移过来,而且是某段区间的和,故可以用前缀和优化到
//dp : a array of zeros longer than M
dp[0] = 1;
for(int i = 1; i <= N; i += 1){
for(int j = v[i]; j <= M; j += 1) dp[j] += dp[j - v[i]]; //prefix sum
for(int j = M; j >= (c[i] + 1) * v[i]; j -= 1) dp[j] -= dp[j - (c[i] + 1) * v[i]];
}加强版:设
f[i][j]表示不使用第i种物品时,总重量为j的方案数
在上面得到 i=N 时的 dp 数组时,可以将操作反向,重新得到 i=N-1 时的 dp 数组
//tmp: another array longer than M
for(int i = 1; i <= N; i += 1){
for(int j = 0; j <= M; j += 1) tmp[j] = dp[j];
for(int j = (c[i] + 1) * v[i]; j <= M; j += 1) tmp[j] += tmp[j - (c[i] + 1) * v[i]];
for(int j = M; j >= v[i]; j -= 1) tmp[j] -= tmp[j - v[i]];
//now, tmp[j] is f(i, j)
}多重背包求最值
朴素版是三重循环 II 怎么把多重背包问题变成一个 01 背包问题?朴素想法是拆分,一个一个拆,但这样会超时。 使用二进制枚举优化,比如说一个数 ,最少用几个数(选或不选两种情况)就可以表示出来 内的所有数呢?答案是 ,分成 , 这样的数,核心代码看模板
int f[M];
int w[N], v[N];
int n, m;
int main()
{
scanf("%d%d", &n, &m);
int cnt = 0;
for (int i = 1; i <= n; i++)
{
int a, b, s;
scanf("%d%d%d", &a, &b, &s);
int k = 1;
while (k <= s)
{
cnt ++;
v[cnt] = a * k;
w[cnt] = b * k;
s -= k;
k *= 2;
}
if (s > 0)
{
cnt ++;
v[cnt] = a * s;
w[cnt] = b * s;
}
}
for (int i = 1; i <= cnt; i++)
for (int j = m; j >= v[i]; j--)
f[j] = max(f[j], f[j - v[i]] + w[i]);
printf("%d\n", f[m]);
return 0;
}III 数据范围比较大时需要使用单调队列优化。 核心思路是把 f[m] 分成若干类,按什么分呢?比如当前要枚举的物品的体积是 ,那么按 即余数来分类(划分等价类),因为 。因为这一类最多有 个物品,所以滑动窗口的大小为 。 (k - q[hh]) / v * w:由于 q[hh] 存的是 j - sv,而这里用 k 表示体积那么一共有 (k - q[hh]) / v 个此物品,他的价值为 (k - q[hh]) / v * w。(这句话暂时看不懂) 难点在于不理解单调队列里存的元素是什么含义,首先它是体积,但具体的变化过程还不清晰
复制一些别人的题解:
所以,我们可以得到
dp[j] = dp[j]
dp[j+v] = max(dp[j] + w, dp[j+v])
dp[j+2v] = max(dp[j] + 2w, dp[j+v] + w, dp[j+2v])
dp[j+3v] = max(dp[j] + 3w, dp[j+v] + 2w, dp[j+2v] + w, dp[j+3v])
...
但是,这个队列中前面的数,每次都会增加一个 w ,所以我们需要做一些转换
dp[j] = dp[j]
dp[j+v] = max(dp[j], dp[j+v] - w) + w
dp[j+2v] = max(dp[j], dp[j+v] - w, dp[j+2v] - 2w) + 2w
dp[j+3v] = max(dp[j], dp[j+v] - w, dp[j+2v] - 2w, dp[j+3v] - 3w) + 3w
...
这样,每次入队的值是 dp[j+k*v] - k*w带注释的代码:
const int N = 1010, M = 20010;
int q[M]; // s的最大值为20000,v的最小值为1,所以队列里面最多是会有200010个元素的
int n, m;
int f[N][M];
int main(){
cin >> n >> m;
for (int i = 1; i <= n; ++ i) {
int v, w, s;
cin >> v >> w >> s;
for (int j = 0; j < v; ++ j) {
int hh = 0, tt = -1;
for (int k = j; k <= m; k += v) {
if (hh <= tt && q[hh] < k - s * v) hh ++; // 判断单调队列中的最大元素是否已经滑出窗口
f[i][k] = f[i - 1][k]; // 不放物品i
if (hh <= tt) f[i][k] = max(f[i][k], f[i - 1][q[hh]] + (k - q[hh]) / v * w); // 放物品i
while (hh <= tt && f[i - 1][q[tt]] + (k - q[tt]) / v * w <= f[i - 1][k]) tt --; // 更新单调的队列
q[++ tt] = k; // 更新单调的队列 进队的是 j + x * v
}
}
}
cout << f[n][m] << endl;
return 0;
}优化为一维:
const int N = 1010, M = 20010;
int n, m;
int v[N], w[N], s[N];
int f[2][M];
int q[M];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; ++ i) cin >> v[i] >> w[i] >> s[i];
for (int i = 1; i <= n; ++ i)
{
for (int r = 0; r < v[i]; ++ r)
{
int hh = 0, tt = -1;
for (int j = r; j <= m; j += v[i])
{
while (hh <= tt && j - q[hh] > s[i] * v[i]) hh ++ ;
while (hh <= tt && f[(i - 1) & 1][q[tt]] + (j - q[tt]) / v[i] * w[i] <= f[(i - 1) & 1][j]) -- tt;
q[ ++ tt] = j;
f[i & 1][j] = f[(i - 1) & 1][q[hh]] + (j - q[hh]) / v[i] * w[i];
}
}
}
cout << f[n & 1][m] << endl;
return 0;
}砝码称重
N个砝码,一个天平,一共能称出几个不同正整数?
背包 dp 问题,f[i][j] 表示从前 i 个选,重量为 j 是否可行。状态计算:不选 f[i-1][j],选放左边 f[i-1][abs(j-w)],放右边 f[i-1][j+w],三者取或。
f[0][0] = 1;
for (int i = 1; i <= n; i++)
for (int j = 0; j <= sum; j++)
{
f[i][j] = f[i - 1][j];
if (w[i] == j) f[i][j] = 1;
if (f[i - 1][j + w[i]]) f[i][j] = 1;
else if (f[i - 1][abs(j - w[i])]) f[i][j] = 1;
}转化为背包 + 分治
意外惊喜 某电商平台举办了一个用户抽奖活动,奖池中共有若干个礼包,每个礼包中包含一些礼物。
present[i][j]表示第i个礼包第j件礼(下标从 0 开始)物的价值。抽奖规则如下:
- 每个礼包中的礼物摆放是有顺序的,你必须从第
0件礼物开始打开;- 对于同一个礼包中的礼物,必须在打开该礼包的第
i个礼物之后,才能打开第i+1个礼物;- 每个礼物包中的礼物价值 非严格递增。 参加活动的用户总共可以打开礼物
limit次,请返回用户能够获得的 最大 礼物价值总和。
注意到有一个结论:不可能出现有两个数组都选了一部分的情况,一定是要么都选完,要么一个选完另外一个不选。枚举这个没有选完的数组,其余的转化为 0-1 背包 。 但这样做时间复杂度为 (0-1 背包 * 枚举每个物品),需要优化。(难点在于怎么优化掉重复计算的背包,因为取 max 值无法撤销,但是我们需要从把礼包当成整体 -> 枚举前缀 -> 恢复为整体,这里包含了撤销的思想) 使用分治优化 ,递归计算 0-1 背包。(如果只剩一个,就枚举前缀,然后当其它礼包都是已经计算好的 0-1 背包;否则,分成两半,先算左侧的背包,带着计算好的结果递归右侧;还原,计算右侧,再递归左侧) 时间复杂度分析,基于归并排序的基础上,多了一个 的循环,base case 复杂度单独算,总共为
int f[12][1050]; // 用 id 记录递归树每一层的结果 最多不超过 log_2(2000)
int sz[2005], val[2005];
class Solution {
public:
int n;
int find(vector<vector<int>>& present, int limit, int id, int L, int R)
{
int re = 0;
if (L == R)
{
int s = 0, v = 0;
re = f[id][limit];
for (auto& x: present[L])
{
// 背包
s ++;
v += x;
if (s > limit) break;
re = max(re, f[id][limit - s] + v);
}
return re;
}
// 分治
int mid = (L + R) / 2;
for (int i = 0; i <= limit; i++)
f[id + 1][i] = f[id][i];
for (int k = L; k <= mid; k++)
for (int i = limit; i >= sz[k]; i--)
f[id + 1][i] = max(f[id + 1][i], f[id + 1][i - sz[k]] + val[k]);
re = max(re, find(present, limit, id + 1, mid + 1, R));
for (int i = 0; i <= limit; i++)
f[id + 1][i] = f[id][i];
for (int k = mid + 1; k <= R; k++)
for (int i = limit; i >= sz[k]; i--)
f[id + 1][i] = max(f[id + 1][i], f[id + 1][i - sz[k]] + val[k]);
re = max(re, find(present, limit, id + 1, L, mid));
return re;
}
int brilliantSurprise(vector<vector<int>>& present, int limit) {
for (int i = 0; i <= limit; i++) f[0][i] = 0;
n = present.size();
for (int i = 0; i < n; i++)
{
val[i] = 0;
sz[i] = present[i].size(); // 存 size
for (int j = 0; j < sz[i]; j++)
val[i] += present[i][j]; // 存 sum
}
return find(present, limit, 0, 0, n - 1);
}
};异或和也能转化为背包?!
给你一个长为
n的数组a,输出它的所有非空子序列的元素和的异或和
这原来是个背包问题啊
f[i][j]表示前i个数选出元素和为j的方案数的奇偶性f[0][0]=1f[i+1][j]=f[i][j]^f[i][j-a[i]]- 答案为
f[n][j]=1的j的异或和
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d", &a[i]);
f[0] = 1;
for (int i = 0; i < n; i++)
for (int j = 1 << 16; j >= a[i]; j--)
f[j] ^= f[j - a[i]];
int res = 0;
for (int i = 0; i < 1 << 16; i++)
if (f[i] == 1) res ^= i;
printf("%d\n", res);
return 0;
}背包问题的翻译
CF543A 有
n个程序员,每个程序员都可以写任意行代码,总共要编写m行代码,这m行代码可以由多个程序员来编写。但是第i个程序员在一行代码中会出现a[i]个 bug。现在希望知道有多少种方案能使得这m行代码中的 bug 的数量不超过b个。
现在有一个体积为 b 的背包,有 n 个物品,第 i 个物品的体积为 a[i],个数有无限个。要求在这 n 个物品中取恰好 m 个物品,且背包能装下的方案有多少种,答案模上 p。
二维费用背包 + 完全背包求方案数
f[0][0] = 1;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
for (int k = a[i]; k <= b; k++)
f[j][k] = (f[j][k] + f[j - 1][k - a[i]]) % p;
int res = 0;
for (int i = 0; i <= b; i++) res = (res + f[m][i]) % p;01 背包变形题
P2340 选
n个人,使得情商和及智商和都是非负数,输出最大的二者总和
自己想的时候没有想到转化为背包问题,怎么分析呢?关键在于每个人只有选或不选两种状态,据此考虑背包。首先背包容量肯定是 n,因为是 n 个人。其次,体积和价值怎么定?
把智商看成体积,情商看成价值。转化为 f[i][j] 表示前 i 个人,智商和为 j 时情商和的最大值
两个问题
- 转移的时候,智商值可能为负数,会影响枚举顺序:故特判
- 下标为负,可能越界:加偏移量
memset(dp, -0x3f, sizeof dp);
dp[400000] = 0;
for(int i = 1; i <= n; i ++)
{
if(a[i].iq >= 0)
for(int j = 800000; j >= a[i].iq; j --)
dp[j] = max(dp[j], dp[j-a[i].iq] + a[i].eq);
else
for(int j = 0; j <= 800000 + a[i].iq; j ++)
dp[j] = max(dp[j], dp[j-a[i].iq] + a[i].eq);
}
for(int i = 400000; i <= 800000; i ++)
if(dp[i] > 0)
ans = max(ans, i + dp[i] - 400000);背包 + 容斥
洛谷 P1450 [HAOI2008] 硬币购物 有
4种硬币,给出n次购物,每次给d[i]个i种硬币,问凑s元方案数s,c[i],d[i]都是1e5,n为1000
这题不能每次询问都做一次完全背包,那怎么办呢?能不能先做一次不带限制的完全背包,然后...
假如只有一种硬币有限制,凑 s 元的方案就包含了 d[i]+1, d[i]+2, ... 种 i 硬币的,把它们减去就好了,这就是一个容斥原理!先选定 (d+1)*v 的体积,剩下 s-(d+1)*v 的背包没有任何限制,太妙了
while (T -- ) {
for (int i = 0; i < 4; i++) {
cin >> d[i];
}
cin >> s;
LL res = f[s];
for (int i = 1; i < 1 << 4; i++) {
LL t = s;
for (int j = 0; j < 4; j++) {
if (i >> j & 1) {
t -= c[j] * (d[j] + 1);
}
}
if (t < 0) {
continue;
}
if (__builtin_popcount(i) % 2) {
res -= f[t];
} else {
res += f[t];
}
}
cout << res << endl;
}石子合并也能是背包
LC1049 每次选两块石头
x和y,若x==y,则粉碎,否则,剩下一个abs(x-y)的石头,问最后剩下的最小重量
本质是给数组的数字添加正负号,求最后结果的最小值(可以手玩一下样例来观察出这个性质)。进而转化为求不超过 sum/2 的最大体积,就是经典背包问题
数据结构优化 DP
最大上升子序和
选出数组的一个严格上升子序列,使得子序列和最大,问最大和是多少
最长上升子序列问题,分析思路是基于 dp 的,思考状态定义:f[i] 表示所有由前 i 个数构成且最后一个元素是 i 的严格上升子序列的集合。怎么划分?可以以倒数第二个数是谁来分类(无,a[1],...,a[i-1]),有些集合可能不存在。状态计算就是 max(f[k])+a[i]。 如何优化?在 i 前找到比它小的数且让 f[k] 最大,这种操作可以用数据结构优化,求前缀最大和用树状数组,求任意区间最大值用线段树。每个 a[i] 都在 1e9 的范围,我们要进行离散化,找出 j < i 且 a[j] < a[i] 中 f[j] 的最大值,相当于以 a[i] 这个数,映射到一个树状数组的下标,存的值就是对应的 f[i]。
// 离散化+前缀最大值的树状数组
for (int i = 0; i < n; i++) scanf("%d", &w[i]);
memcpy(q, w, sizeof w);
sort(q, q + n);
m = unique(q, q + n) - q;
LL res = 0;
for (int i = 0; i < n; i++)
{
int x = lower_bound(q, q + m, w[i]) - q + 1;
LL sum = query(x - 1) + w[i];
res = max(res, sum);
add(x, sum);
}裁剪序列
给定一个长度为
N的序列A,要求把该序列分成若干段,在满足“每段中所有数的和”不超过M的前提下,让“每段中所有数的最大值”之和最小。 试计算这个最小值。
把数组分成若干段,每段的和不超过 ,并让每段中最大值之和最小。 考虑 dp 怎么来分析:状态定义很好确定,状态计算要划分集合,一般找最后一个不同点,我们可以看最后一段,按最后一段的长度来分类。 拿出一个子集,假如最后一段的长度为 ,那么前 个数怎么划分是随意的,那么 f[i]=f[i-k]+max。 考虑优化:先求出 的最大值,即最后一段起点的最小值 ,有如下结论:(1)对于 [1...i] 的划分方案,[1...j] 的划分方案,当 i<j,有后者大于等于前者(前者的方案都能在后者中找到),即元素越多代价越大。(2)有可能作为答案的点一定是在 [j...i] 内,我们找到一个单调递减 a[k] 序列,这个序列中的每一个点(确定一个 后,我们一定要选最小起点)。 如何维护这个单调递减的序列?首先我们需要对每个下标 都维护一个最小的 ,使得 sum[j...i]<=M,这是一个双指针问题,但要先证明随着尾指针后移,头指针也一定后移(由每个数都非负得证)。接下来我们要在这个滑动窗口中维护一个单点递减的序列,这是经典单调队列维护问题。 然后再考虑我们区间右移的时候,要么从队头一个个删,要么从队尾一个个删,每个元素最多入队一次出队一次,因此我们需要维护一个集合,支持动态求最小值,删除一个数,插入一个数,可以用平衡树(multiset)实现。 代码实现上,可以先写好双指针逻辑,再插入单调队列的逻辑,最后写 multiset 的逻辑(由于 是最后一段的起点,因此 dp 公式是 f[i] = f[j - 1] + w[q[hh]];):
multiset<LL> s; // 单调队列有 k 个数时 维护的是 k - 1 个区间 (如 f[k] + ak+1)
// ...
void remove(LL x)
{
auto it = s.find(x);
s.erase(it); // 如果有多个取值 只删除一个
// 直接调用 s.erase(x) 会把所有都删除
}
for (int i = 1, j = 1; i <= n; i++) // 双指针维护对确定的 i,j 的范围
{
sum += w[i];
while (sum > m)
{
sum -= w[j++];
if (hh <= tt && q[hh] < j) // 维护单调队列的左端
{
if (hh < tt) remove(f[q[hh]] + w[q[hh + 1]]); // 单调队列中大于一个元素时才删除
hh++;
}
}
while (hh <= tt && w[i] >= w[q[tt]]) // 维护单调队列的右端
{
if (hh < tt) remove(f[q[tt - 1]] + w[q[tt]]);
tt--;
}
q[++tt] = i; // 入队
if (hh < tt) s.insert(f[q[tt - 1]] + w[q[tt]]); // 起码 2 个元素时 更新这一段区间的值
f[i] = f[j - 1] + w[q[hh]]; // 由 dp 公式
if (s.size()) f[i] = min(f[i], *s.begin());
}前缀和或滑窗 优化多重背包
给你一个下标从 0 开始的非负整数数组
nums和两个整数l和r。 请你返回nums中子多重集合的和在闭区间[l, r]之间的 子多重集合的数目 。 由于答案可能很大,请你将答案对10^(9)+7取余后返回。 子多重集合 指的是从数组中选出一些元素构成的 无序 集合,每个元素x出现的次数可以是0, 1, ..., occ[x]次,其中occ[x]是元素x在数组中的出现次数。 注意:
- 如果两个子多重集合中的元素排序后一模一样,那么它们两个是相同的 子多重集合 。
- 空 集合的和是
0。nums的和不超过2 * 10^(4)。
题意即给定 k 种物品,个数有限,放进容积为 r 的背包的方案数。本题的 k 是 级别,可以使用 的算法过
// 前缀和优化
class Solution {
public:
const int MOD = 1e9 + 7;
int countSubMultisets(vector<int>& nums, int l, int r) {
int n = nums.size();
vector<int> f(r + 1);
unordered_map<int, int> cnt;
for (int x: nums) cnt[x] ++;
f[0] = 1;
for (auto &[x, y]: cnt)
{
if (x == 0) continue;
for (int j = x; j <= r; j++)
f[j] = (f[j] + f[j - x]) % MOD;
for (int j = r; j >= (y + 1) * x; j--)
f[j] = (f[j] - f[j - (y + 1) * x]) % MOD;
}
int res = 0;
for (int i = l; i <= r; i++) res = (res + f[i]) % MOD;
res = (res * (1LL * (cnt[0] + 1))) % MOD;
return (res + MOD) % MOD;
}
};核心:
- 对
0做特判,体现在最后 f[i][j]和f[i][j-v]的转移方程对比,少了一个f[i-1][j-v*(c+1)],多了一个f[i-1][j],这启示我们可以用滑窗或者前缀和来维护这一段区间和,就可以O(1)转移了
// 滑窗版本,需要按取模的余数分类
class Solution {
public:
const int MOD = 1e9 + 7;
int countSubMultisets(vector<int>& nums, int l, int r) {
int n = nums.size();
unordered_map<int, int> cnt;
int mx = 0;
for (int x: nums) cnt[x] ++, mx = max(mx, x);
int f[(int)cnt.size() + 1][r + 1], g[mx + 1];
memset(f, 0, sizeof f);
memset(g, 0, sizeof g);
f[0][0] = 1;
int i = 0;
for (auto &[x, y]: cnt)
{
if (x == 0) continue;
i ++;
for (int j = 0; j <= mx; j++) g[j] = 0;
for (int j = 0; j <= r; j++)
{
int md = j % x;
g[md] = (g[md] + f[i - 1][j]) % MOD;
int t = j - x * (y + 1);
if (t >= 0) g[md] = (g[md] - f[i - 1][t]) % MOD;
f[i][j] = g[md];
}
}
int res = 0;
for (int j = l; j <= r; j++) res = (res + f[i][j]) % MOD;
res = (res * (1LL * (cnt[0] + 1))) % MOD;
return (res + MOD) % MOD;
}
};
// 核心代码
// 当前需要使用哪个滑动窗口
int md = j % v[i];
// 滑动窗口滑动一步
g[md] += f[i - 1][j];
g[md] -= f[i - 1][j - v[i] * (a[i] + 1)];
// 把滑动窗口的值赋给 dp 数组
f[i][j] = g[md];树形 DP
最小高度树
这道题首先求出以 0 为根时各子树的高度,记录在 h[] 数组中;dp 的时候是先求出 u 的子节点的最大高度和次大高度,然后记录 f[u];之后换根时注意了,**是先更新了 h[u] 再去 dp(v)!**这样在 dp(v) 的时候,h[] 刚好就是以 v 为根时各子树的高度
为什么:换根时只会影响 h[u],因此先更新 h[u] 才是正确的
求树上长度恰好为 k 的路径个数
分类讨论
一是节点
u到子树内长为k的链f[u][k]枚举
u的每两个子节点,把链拼起来,巧妙做法是sum{(f[u][k-i]-f[v][k-i-1]) * f[v][i-1]}- 意思是在
v子树中选长为i-1的链,然后和u子树中长为k-i的链匹配,但是要先减去v中的链,避免算重
- 意思是在
void dfs(int u, int fa) {
f[u][0] = 1;
for (int v: g[u])
if (v != fa) {
dfs(v, u);
for (int i = 0; i < k; i++)
f[u][i + 1] += f[v][i];
}
res += f[u][k];
LL ans = 0;
for (int v: g[u])
if (v != fa)
for (int i = 1; i < k; i++)
ans += f[v][i - 1] * (f[u][k - i] - f[v][k - i - 1]);
res += ans / 2;
}换根 DP 解决白色点-黑色点的最大值
CF1324F 对于每个节点
u,选出一个包含u的连通子图,设子图中白点个数为cnt1,黑点个数为cnt2,请最大化cnt1-cnt2。并输出这个值。
法一:
固定根时,定义 f[v] 表示以 v 为根子树的最大值,那么对于每个子树,f[v] += max(f[to], 0)
换根,只会改变 f[v] 和 f[to] 的值,可以根据它的值是否为 0 来得知原来是怎么转移的,然后更新之后 dp 子树,最后回溯
void dfs(int u, int fa) {
f[u] = a[u];
for (int v: g[u])
if (v != fa) {
dfs(v, u);
f[u] += max(f[v], 0);
}
}
void dfs2(int u, int fa) {
res[u] = f[u];
for (int v: g[u])
if (v != fa) {
f[u] -= max(f[v], 0);
f[v] += max(f[u], 0);
dfs2(v, u);
// rollback
f[v] -= max(f[u], 0);
f[u] += max(f[v], 0);
}
}法二:直接在 a[i] 上计算,换根时
- 如果
a[to] > 0,那么a[v]的答案包含a[to],取最大值max(a[to], a[v]) - 否则,
a[v]的答案不包含a[to],就可以选或不选max(a[to], a[v]+a[to])
void dfs(int now, int pre) {
for (auto &to:v[now]) {
if (to == pre)
continue;
dfs(to, now);
if (a[to] > 0)
a[now] += a[to];
}
}
void dfs2(int now, int pre) {
for (auto &to:v[now]) {
if (to == pre)
continue;
if (a[to] > 0)
a[to] = max(a[to], a[now]);
else
a[to] = max(a[to], a[now] + a[to]);
dfs2(to, now);
}
}求 sigma(d[i]*a[i]) for 每个点为根
当根从 u 换到 v 时,以 v 为根子树的贡献各减少 1,共减少 s[v],其余部分贡献各增加 1,共增加 sum-s[v],因此转移方程为 f[v]=f[u]+sum-2*s[v]
- 这题注意的点在于维护一个点权和用于转移,进阶版:求
sigma(d[i]^2*a[i])
void dfs(int u, int fa) {
s[u] = a[u], f[u] = 0;
for (int v: g[u])
if (v != fa) {
dfs(v, u);
s[u] += s[v];
f[u] += f[v] + s[v];
}
}
void dfs2(int u, int fa) {
if (fa) f[u] = f[fa] + sum - 2 * s[u];
for (int v: g[u])
if (v != fa) dfs2(v, u);
}二叉树灯饰——状态设计
LCP64 二叉树:0 表示关灯,1 表示开灯
- 操作 1:切换当前根节点状态
- 操作 2:切换当前子树所有节点状态
- 操作 3:切换根节点和左右子节点的状态 问使得二叉树所有点状态都为 0,最小操作次数
本题核心在于观察操作 2 和 3,发现如果左右子节点在操作后状态不同,将没有操作使得它们相同(同亮同灭)
基于这个观察设计状态:f(root, 0/1, 0/1) 表示该子树的根是否亮,该子树除根外的所有节点是否亮
class Solution {
public:
const int INF = (int)1e9;
vector<int> dp(TreeNode *root) {
if (root == nullptr) return {0, 0, 0, 0};
vector<int> L = dp(root->left), R = dp(root->right);
vector<int> res = {INF, INF, INF, INF};
// 枚举以子节点为根的子树的状态,a 表示子节点的状态,b 表示除子节点外的其它节点的状态
for (int a = 0; a < 2; a++)
for (int b = 0; b < 2; b++) {
int from = b * 2 + a;
int c = root->val;
// 每种操作最多做一次,因此用二进制枚举做了哪些操作
for (int i = 0; i < 8; i++) {
int x = i & 1, y = i >> 1 & 1, z = i >> 2 & 1;
// 子节点只受操作 2 和 3 的影响
int aa = (y ^ z ? 1 - a : a);
// 除子节点外的其它节点只受操作 2 的影响
int bb = (y ? 1 - b : b);
// 当前节点受所有操作影响
int cc = (x ^ y ^ z ? 1 - c : c);
// 除根外的节点要保持一致,否则后续没有操作能让它们一致
if (aa != bb) continue;
res[aa * 2 + cc] = min(res[aa * 2 + cc], L[from] + R[from] + x + y + z);
}
}
return res;
}
int closeLampInTree(TreeNode* root) {
return dp(root)[0];
}
};每个点最多保留 k 条边,求删边后树的最大权值和
对于节点 和一条边 ,考虑选或不选
- 不选,则转化为对于节点 及其儿子,最多选 条
- 选,则转化为对于节点 及其儿子,最多选 条
一开始我们可以都不选,然后再选出可以最大化增量的那些边,怎么求出来呢?
把选的减去不选的差值()放入数组中排序,然后选择前 个大于 0 的值即可
原题见 LC3367
树中删一条链,最大化剩下的连通分支数
原题在 CF2050G 公式是 ,其中 是链的边数
据此设计 DP,一个点
- 要么链以它为开头
- 要么链经过它,头尾都在子树中
因此定义 表示第一种情况时的答案,第二种情况可以顺便算出来
// 度数和 - 2*k 其中 k 是链的边数
auto dfs = [&](auto &&dfs, int u, int fa) -> void {
f[u] = g[u].size(); // 只删自己
int m1 = -1, m2 = -1;
for (int v: g[u]) {
if (v != fa) {
dfs(dfs, v, u);
f[u] = max(f[u], f[v] + (int)g[u].size() - 2); // 多了一条边 + 一个点
m2 = max(m2, f[v]);
if (m1 < m2) {
swap(m1, m2);
}
}
}
res = max(res, f[u]);
if (m2 != -1) {
res = max(res, m1 + m2 + (int)g[u].size() - 4); // 多了一个点 + 两条边
}
};优化 DP
带权区间,最多选 4 个,求权值和最大,不重叠且字典序最小的方案
定义 表示在下标 中至多选 个的最大和,区间排序后维护前缀最大值,二分找到最右边的合法区间转移即可,这个思路很熟悉,但是代码不好写,需要学习编码技巧
写法一:灵神版本
class Solution {
public:
struct Node {
int l, r, w, i;
};
using LL = long long;
vector<int> maximumWeight(vector<vector<int>>& intervals) {
int n = intervals.size();
vector<Node> a(n);
for (int i = 0; i < n; i++) {
a[i] = {intervals[i][0], intervals[i][1], intervals[i][2], i};
}
ranges::sort(a, {}, &Node::r);
vector<array<pair<LL, vector<int>>, 5>> f(n + 1);
for (int i = 0; i < n; i++) {
auto [l, r, w, idx] = a[i];
int k = lower_bound(a.begin(), a.begin() + i, l, [](Node &t, int val) { return t.r < val; }) - a.begin();
for (int j = 1; j < 5; j++) {
LL s1 = f[i][j].first;
// 为什么是 f[k] 不是 f[k+1]:上面算的是 >= l,-1 后得到 < l,但由于还要 +1,抵消了
LL s2 = f[k][j - 1].first + w;
if (s1 > s2) {
f[i + 1][j] = f[i][j]; // 转移来源一
continue;
}
vector<int> new_id = f[k][j - 1].second;
new_id.push_back(idx);
ranges::sort(new_id);
if (s1 == s2 && f[i][j].second < new_id) {
new_id = f[i][j].second;
}
// 转移来源二
f[i + 1][j] = {s2, new_id};
}
}
return f[n][4].second;
}
};写法二:TsReaper 版本,但不太理解为什么把区间拆开来存,虽然在前缀最大值的思路下,二分找到的是右端点还是左端点不影响答案
class Solution {
public:
using PII = pair<int, int>;
using LL = long long;
vector<int> maximumWeight(vector<vector<int>>& intervals) {
int n = intervals.size();
// a 中保存所有关键点,第一维是坐标,第二维是关键点对应的区间编号
// 若编号为 -1 表示这是左端点,若编号非负表示这是右端点
// 哨兵元素,防止讨论边界情况
vector<PII> a{{-1, -1}};
for (int i = 0; i < n; i++) {
auto &t = intervals[i];
a.push_back({t[0], -1});
a.push_back({t[1], i});
}
ranges::sort(a);
n = a.size();
// DP 值是一个五维的数组,第一维是权值取负数,后面四维是方案
// 此时,取字典序最小的数组就是答案
array<LL, 5> f[n][5];
const LL INF = 1e18;
for (int j = 1; j <= 4; j++) {
f[0][j] = {INF, INF, INF, INF, INF};
}
f[0][0] = {0, INF, INF, INF, INF};
for (int i = 1; i < n; i++) {
for (int j = 0; j <= 4; j++) {
f[i][j] = f[i - 1][j];
}
int idx = a[i].second;
if (idx >= 0) {
// 这是一个右端点,通过二分找出 k 的最大值
int L = intervals[idx][0];
int l = 0, r = i - 1;
while (l < r) {
int mid = l + r + 1 >> 1;
if (a[mid].first < L) {
l = mid;
} else {
r = mid - 1;
}
}
for (int j = 1; j <= 4; j++) {
auto tmp = f[l][j - 1];
tmp[0] -= intervals[idx][2];
tmp[j] = idx;
// 为了让方案字典序最小,方案内部也要排序一下
ranges::sort(tmp);
f[i][j] = min(f[i][j], tmp);
}
}
}
array<LL, 5> res = {INF, INF, INF, INF, INF};
for (int j = 1; j <= 4; j++) {
res = min(res, f[n - 1][j]);
}
vector<int> ans;
for (int j = 1; j <= 4; j++) {
if (res[j] < INF) {
ans.push_back(res[j]);
}
}
return ans;
}
};后缀和优化
参考 的解法,用到了后缀和来优化
class Solution {
public:
int ways(vector<string>& pizza, int k) {
int m = pizza.size(), n = pizza[0].size();
LL f[m + 1][n + 1];
memset(f, 0, sizeof f);
int s[m + 1][n + 1];
memset(s, 0, sizeof s);
for (int i = m - 1; i >= 0; i--)
for (int j = n - 1; j >= 0; j--)
{
s[i][j] = s[i][j + 1] + s[i + 1][j] - s[i + 1][j + 1] + (pizza[i][j] == 'A');
if (s[i][j]) f[i][j] = 1;
}
while (-- k )
{
vector<int> cols(n); // colS[j] 表示 f 第 j 列的后缀和
for (int i = m - 1; i >= 0; i--)
{
LL rows = 0; // f[i] 的后缀和
for (int j = n - 1; j >= 0; j--)
{
LL t = f[i][j];
if (s[i][j] == s[i][j + 1])
f[i][j] = f[i][j + 1];
else if (s[i][j] == s[i + 1][j])
f[i][j] = f[i + 1][j];
else f[i][j] = (rows + cols[j]) % MOD;
rows = (rows + t) % MOD;
cols[j] = (cols[j] + t) % MOD;
}
}
}
return f[0][0];
}
};CF1913D 单调栈优化 DP
元素值互不相同的数组,可以选择一个连续子数组,保留其中的最小值,其它删掉。可操作任意次,问能得到不同的数组的个数。
思路:被删除的元素不一定是连续的 -> 子序列问题
转换为统计剩余子序列的个数 -> DP
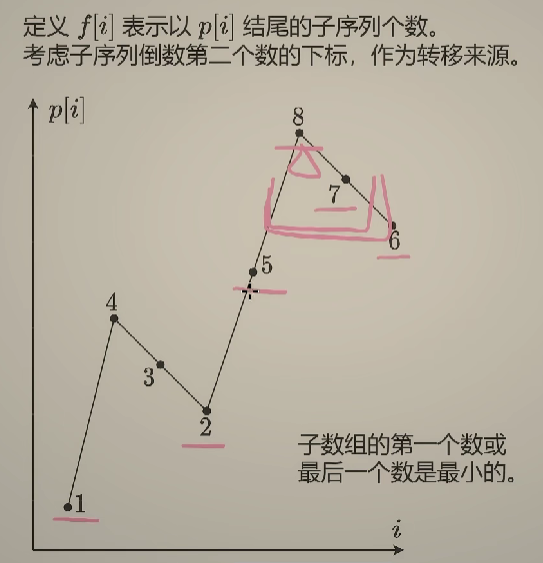
经典套路:定义 f[i] 表示以 p[i] 结尾的子序列个数,然后考虑倒数第二个数可以是哪个
特点:要操作的子数组的第一个数或者最后一个数一定是最小的
因此转移来源有两部分
- 最后一个数最小时,倒数第二个数可以是它左边比它大的数
- 第一个数最小时,需要用单调栈维护这些数(手玩样例可以发现)
在当前数入栈前,需要把栈中比它大的数都出栈
特殊情况:若单调栈为空,表明当前这个数可以单独作为子数组,f 值 +1
维护 f的前缀和,以及栈中元素对应的 f 值的和
能够作为结尾的数恰好是最后留在单调栈中的数字
cin >> n;
for (int i = 0; i < n; i++) cin >> a[i];
vector<LL> s(n + 1), f(n);
stack<int> st;
LL sum = 0; // 单调栈的元素的 f 值和
for (int i = 0; i < n; i++)
{
while (st.size() && a[st.top()] > a[i])
{
sum -= f[st.top()];
st.pop();
}
int j = st.empty() ? 0 : st.top() + 1;
f[i] = (sum + s[i] - s[j] + st.empty()) % mod;
s[i + 1] = (s[i] + f[i]) % mod;
sum = (sum + f[i]) % mod;
st.push(i);
}
cout << (sum + mod) % mod << endl;求 min(max(最大子段和,| 最小子段和 |))
LCP65 题目意思是,可以把数组的一些数变成相反数,然后最小化数组的
max(最大子段和,最小子段和的绝对值)数据范围和值域都是1000
这种问题的处理方法是数形结合,即用折线图的形式表示前缀和,然后可以发现要求的东西变成了折线图中最高点-最低点(重要技巧!)
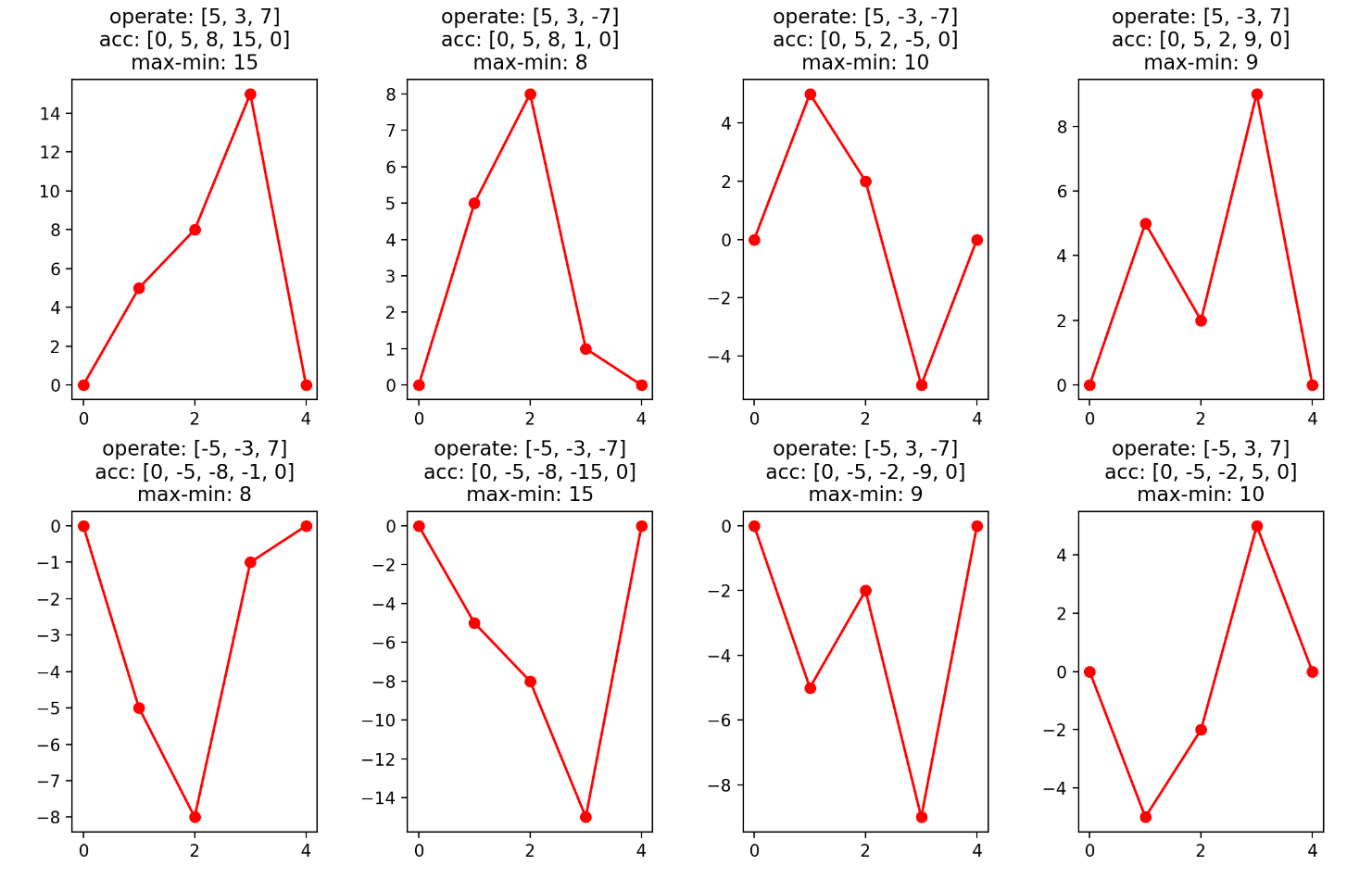
然后,子段和启发我们往 DP 上靠,本题最难的地方在于设计状态!从数据范围入手,值域 1000,再想想折线图的上界是多少?不就是数组的最大值吗?也就是说折线始终会在 [-mx, mx] 内
那么,状态定义就是 f[i][j] 表示考虑前 i 个数,其中某些数字取负,折线图右端点到折线图最低点的纵坐标距离为 j 时,折线图最大值与最小值之差的最小值(这个定义就把值域考虑进去了,最终是 的做法)
状态转移:考虑每个数取正还是取负
取正,折线图向上走,
f[i-1][j]->f[i][j+x]取负,折线图向下走,要考虑会不会产生新的最低点
- 不产生:
f[i-1][j]->f[i][j-x] - 产生:根据定义,
f[i][0]<-f[i-1][j]+x-j
- 不产生:
初始值,f[0][0]=0,其余为无穷,答案为 min(f[n-1])
class Solution {
public:
int unSuitability(vector<int>& operate) {
int mx = ranges::max(operate) * 2 + 1;
vector<int> pre(mx, 0x3f3f3f3f), f(mx);
pre[0] = 0;
for (int x: operate) {
fill(f.begin(), f.end(), 0x3f3f3f3f);
for (int j = 0; j < mx; j++) {
int dis = pre[j];
if (dis == 0x3f3f3f3f) continue; // 无效的长度(无法组成)
if (j + x < mx) f[j + x] = min(f[j + x], max(dis, j + x));
if (j >= x) f[j - x] = min(f[j - x], dis);
else f[0] = min(f[0], dis + x - j);
}
swap(pre, f);
}
return ranges::min(pre);
}
};前缀 max 优化 DP
LCP57
3×3网格上,每秒每个位置最多出现一只地鼠,地鼠出现的格式为(t,x,y),t=0时锤子在(1,1),每移动一格需要1s,问最多打到几只地鼠。t的取值范围为1e9
坑点在于,t=0 时其他位置的地鼠是打不到的
状态设计:f[i] 表示考虑前 i 只地鼠(按出现时间顺序排序),保证打第 i 只时,最多能打多少只
转移的话,考虑上一只打的地鼠是谁就可以了,只要相差时间不小于移动距离即可。但这样做是 的,怎么优化?考虑到网格的最远距离只有 4,因此相差时间大于 4 的,就一定能转移,那么这一段就用前缀 max 优化。需要枚举的数量变成了 4×9=36,总的复杂度就是
class Solution {
public:
int getMaximumNumber(vector<vector<int>>& moles) {
// 把所有时间 0 出现的地鼠排除
vector<vector<int>> A;
bool flag = false;
for (auto &mole : moles) {
if (mole[0] == 0) {
// 看一下有没有时间 0 位于 (1, 1) 的地鼠,一开始就能打
if (mole[1] == 1 && mole[2] == 1) flag = true;
} else {
A.push_back(mole);
}
}
// 初始位置位于 (1, 1)
A.push_back(vector<int>{0, 1, 1});
int n = A.size();
sort(A.begin(), A.end());
vector<int> f(n), g(n);
int ans = 0;
for (int i = 1; i < n; i++) {
f[i] = -1e8;
for (int j = i - 1; j >= 0; j--) {
int t = A[i][0] - A[j][0], d = abs(A[i][1] - A[j][1]) + abs(A[i][2] - A[j][2]);
// 能从任何位置移过来,用前缀 max 更新答案
if (t > 4) { f[i] = max(f[i], g[j] + 1); break; }
// 虽然有时间限制,但移过来能来得及,更新答案
else if (d <= t) f[i] = max(f[i], f[j] + 1);
}
ans = max(ans, f[i]);
g[i] = max(g[i - 1], f[i]);
}
return ans + (flag ? 1 : 0);
}
};划分数字的方案数
LC1977 给一个字符串
num,一个正整数数组,非递减,每个数拼起来得到num,问有多少种构造数组的方案,要求 做法
定义 f[i][j] 表示考虑了 [0,j] 这一段,最后一段数是 [i,j],转移的话就考虑前一段,就是 sigma(f[k][i-1]),由于数位越多,数字越大,得到 i-1-k<=j-i,然后要分情况了,k=2*i-j-1 时,前一段和这一段数位相同,需要比较数字本身,k>=2*i-j 时,连续的一段可以用前缀和累加
好了,怎么比较数字本身呢?这里用到了 lcp(lcp[i][j] 表示从 i 开始的后缀和从 j 开始的后缀的最长公共前缀长度),我们看 lcp[2*i-j-1][i] 的大小,如果等于这一段的长度,说明数字相等,如果小于,那就看第一个不同的位置的大小,这个是好理解的
前缀和这里怎么办呢?观察 f[i][j] 和 f[i][j+1] 的求和式,发现只相差 f[2*i-j-i][i-1] 这一项,于是可以用一个变量来累加就可以了
int numberOfCombinations(string num) {
if (num[0] == '0') {
return 0;
}
int n = num.size();
int lcp[n][n];
memset(lcp, 0, sizeof(lcp));
for (int i = n - 1; i >= 0; i--) {
lcp[i][n - 1] = num[i] == num[n - 1];
for (int j = i + 1; j < n - 1; j++) {
lcp[i][j] = (num[i] == num[j] ? lcp[i + 1][j + 1] + 1 : 0);
}
}
int f[n][n];
memset(f, 0, sizeof(f));
for (int i = 0; i < n; i++) {
f[0][i] = 1;
}
for (int i = 1; i < n; i++) {
if (num[i] == '0') {
continue;
}
int pre = 0;
for (int j = i; j < n; j++) {
int len = j - i + 1;
f[i][j] = pre;
if (i - len >= 0) {
if (lcp[i - len][i] >= len || num[i - len + lcp[i - len][i]] < num[i + lcp[i - len][i]]) {
f[i][j] = (f[i][j] + f[i - len][i - 1]) % MOD;
}
pre = (pre + f[i - len][i - 1]) % MOD;
}
}
}
int res = 0;
for (int i = 0; i < n; i++) {
res = (res + f[i][n - 1]) % MOD;
}
return res;
}逆序对相关的 DP
问
1-n的排列数,满足有k个逆序对
定义 f[i][j] 表示用数值 [1,i],凑出 j 个逆序对的方案数。考虑第 i 个数放的位置,从下标 0 到 i-1,可以发现状态转移上,取的是连续的一段,可以用前缀和优化
此处转移方程为 f[i][j] = sigma(k from 0 to i-1)f[i-1][j-k]
func kInversePairs(n int, k int) int {
const MOD int = 1e9 + 7
f := make([][]int, 2)
for i := range f {
f[i] = make([]int, k + 1)
}
f[0][0] = 1
for i := 1; i <= n; i++ {
cur, pre := i & 1, i & 1 ^ 1
sum := 0
for j := 0; j <= k; j++ {
sum = (sum + f[pre][j]) % MOD
f[cur][j] = sum
if j >= i - 1 {
sum = (sum - f[pre][j - i + 1] + MOD) % MOD
}
}
}
return f[n & 1][k]
}给出若干限制
[end, cnt],表示[0,end]内刚好有cnt个逆序对,问方案数(保证有end==n-1)
定义 f[i][j] 表示从下标 [0,i] 的排列中,恰有 j 个逆序对的方案数。同样考虑下标为 i 的数 a[i],和前面 i 个数的大小,假设比 d 个数小,那么 f[i][j]<-f[i-1][j-d]。当遇到限制时,只计算 f[end][j=cnt] 的值,其它的 f[end][*]=0,这里同样可以用前缀和优化
func numberOfPermutations(n int, requirements [][]int) int {
const MOD int = 1e9 + 7
req := make([]int, n)
for i := 0; i < n; i++ {
req[i] = -1
}
for _, r := range requirements {
req[r[0]] = r[1]
}
if req[0] > 0 {
return 0
}
mx := slices.Max(req)
f := make([][]int, 2)
for i := range f {
f[i] = make([]int, mx + 1)
}
f[0][0] = 1
for i := 1; i <= n; i++ {
pre, cur := i & 1 ^ 1, i & 1
sum := 0
for j := 0; j <= mx; j++ {
sum = (sum + f[pre][j]) % MOD
if req[i - 1] == -1 || req[i - 1] == j {
f[cur][j] = sum
} else {
f[cur][j] = 0
}
if j >= i - 1 {
sum = (sum - f[pre][j - i + 1] + MOD) % MOD
}
}
}
return f[n & 1][req[n - 1]]
}典题
维护后缀最大值?直接把状态定义为后缀最大值!
给一个数组,求最长子序列,使得相邻元素的绝对差构成一个非递减序列,
标签:[相邻元素]、[后缀最值]
定义 表示以 结尾,上一个绝对差为 时的最大长度。那么枚举当前数 ,上一个数为 ,当前绝对差 ,就需要找到 的最大值,这是一个后缀最大值
但实际上不需要这样,直接定义 表示以 结尾,绝对差至少为 的最大长度,那么得到转移方程为
但是如果 ,就会重复累加,怎么办?用一个变量 表示
class Solution {
public:
int longestSubsequence(vector<int>& nums) {
auto [mn, mx] = ranges::minmax(nums);
int d = mx - mn;
int f[mx + 1][d + 1];
memset(f, 0, sizeof(f));
int res = 0;
for (int x: nums) {
int fx = 1;
for (int j = d; j >= 0; j--) {
if (j + x <= mx) {
fx = max(fx, f[x + j][j] + 1);
}
if (x - j >= 0) {
fx = max(fx, f[x - j][j] + 1);
}
f[x][j] = fx;
res = max(res, fx);
}
}
return res;
}
};使得字符串所有出现字母的频次相同的最小操作数
- 要么加一个字符
- 要么删一个字符
- 要么把字符变成字母表的下一个(
z不能变)
本题的特点在于需要枚举最后出现的次数 k,对每个 k 进行一次 的 DP
k 的范围是 到 ,因为保底是都添加到 个
对于第 种字符,要么不保留,全删;要么弄成 个
怎么弄?要么添加,要么看看能否从第 种变过来。注意,一个字符变两次不如一删一增,因此仅需考虑上一种即可
auto calc = [&](int k) {
int f[27][2];
memset(f, 0x3f, sizeof(f));
f[0][0] = 0;
for (int i = 1; i <= 26; i++) {
// 不保留第 i 种
f[i][0] = min(f[i - 1][0], f[i - 1][1]) + cnt[i];
if (cnt[i] >= k) {
// 通过删除使得第 i 种剩 k 个
f[i][1] = min(f[i - 1][0], f[i - 1][1]) + cnt[i] - k;
} else {
// 不够 要么加 要么从 i-1 变过来
int d = k - cnt[i];
// 第 i-1 种未保留 如果能变过来 就省下一次删除
f[i][1] = min(f[i][1], f[i - 1][0] + d - min(d, cnt[i - 1]));
// 第 i-1 种保留了 k 个 多出来的变成第 i 种
f[i][1] = min(f[i][1], f[i - 1][1] + d - min(max(0, cnt[i - 1] - k), d));
}
}
return min(f[26][0], f[26][1]);
};
int res = n; // 最小是全删去
for (int i = 1; i <= n; i++) {
res = min(res, calc(i));
}最长公共上升子序列长度
最长上升子序列问题,定义 f[i][j] 表示所有在 A[1...i] 中和 B[1...i] 中都出现过的且以 B[j] 结尾的公共上升子序列集合。 状态计算:集合划分?分成 A[i] 不包含在公共子序列中的集合(左边)和包含 A[i] 的公共子序列(右边)。左边对应的是所有在 A[1...i-1] 和 B[1...i] 中出现的公共子序列,恰好就是 f[i-1][j]。右边直接求不好求,需要继续划分。按倒数第二个数划分(不存在,B[1],B[2]...B[j-1]),不存在意味着长度为 1,值也是 1。对于第 类,值为 f[i-1][k]+1。为什么?首先由公共的定义,A[i]==B[j],因此去掉不管,只考虑前面的部分,就能得出这个答案了。 朴素做法需要三重循环,考虑优化掉一重循环:我们发现每次循环求得的 maxv 是满足 a[i] > b[k] 的 f[i - 1][k] + 1 的前缀最大值。因此我们可以记录下前面求得的最大值,进而优化掉一重循环。
for (int i = 1; i <= n; i++)
{
int maxv = 1;
for (int j = 1; j <= n; j++)
{
f[i][j] = f[i - 1][j];
if (a[i] == b[j]) f[i][j] = max(f[i][j], maxv);
if (b[j] < a[i]) maxv = max(maxv, f[i - 1][j] + 1);
}
}不同的子序列:随机化
给定一个字符串 和一个字符串 ,请问共有多少个 的不同的子序列等于 。 第一行包含整数 ,表示共有 组测试数据。 每组数据第一行包含字符串 ,第二行包含字符串 。 每组数据输出一行,一个结果,由于结果可能很大,因此输出其对 取模后的值。 , 保证 中的每个字符都是随机生成的。 字符串中只包含小写字母。
分析:经典 DP,优化掉一维,否则超内存;但是 TLE,原因在于复杂度为 ,注意加粗的条件,随机生成意味着 的概率为 ,能不能只枚举 出现的位置呢,时间复杂度降为 ,可以过。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std;
const int N = 10010, MOD = 1e9 + 7;
int f[N];
char a[N], b[N];
int main()
{
int Q;
scanf("%d", &Q);
while (Q -- )
{
scanf("%s%s", a + 1, b + 1);
int n = strlen(a + 1), m = strlen(b + 1);
vector<int> p[26];
for (int i = m; i; i -- ) p[b[i] - 'a'].push_back(i);
memset(f, 0, sizeof f);
f[0] = 1;
for (int i = 1; i <= n; i ++ )
for (int j: p[a[i] - 'a'])
f[j] = (f[j] + f[j - 1]) % MOD;
printf("%d\n", f[m]);
}
return 0;
}最大子段和
给序列,
k,x你需要执行一次操作,选择恰好k个不同位置,元素+x,其余元素-x,求出操作后的最大连续子数组和,考虑空数组,和为0
用 0 1 2 三种状态记录当前在答案字段前,中,后
cin >> n >> k >> x;
for (int i = 0; i < n; i++) cin >> a[i];
for (int i = 0; i <= n; i++)
for (int j = 0; j <= k; j++)
for (int t = 0; t < 3; t++)
f[i][j][t] = -1e18;
f[0][0][0] = 0;
for (int i = 0; i < n; i++)
for (int j = 0; j <= k; j++)
for (int t = 0; t < 3; t++)
{
if (f[i][j][t] == -1e18) continue;
for (int jj = j; jj <= min(k, j + 1); jj++)
{
LL add = a[i] + (j == jj ? -x : x);
for (int tt = t; tt < 3; tt++)
f[i + 1][jj][tt] = max(f[i + 1][jj][tt], f[i][j][t] + (tt == 1 ? add : 0));
}
}
cout << max(f[n][k][1], f[n][k][2]) << endl;任意修改序列的一个数,问之后的 LIS 长度
思路是维护 f[i],表示以 a[i] 结尾的 LIS;维护 g[i],表示以 a[i] 开头的 LIS
然后枚举位置
- 若不是最后一个位置,可以改后面那个数,即
res=max(res, f[i]+1) - 若不是最开始的位置,且当前
a[i]不是0,就可以改前面那个数,即res=max(res, g[i]+1) - 假设有两段,枚举后一段开始的位置,要满足
a[j]-a[i]>1,就可以改中间的数,即res=max(res, f[i]+g[j]+1)
代码细节较多
for (int i = 1; i <= n; i++)
for (int j = 1; j < i; j++)
if (a[j] < a[i]) f[i] = max(f[i], f[j] + 1);
for (int i = n; i >= 1; i--)
for (int j = n; j > i; j--)
if (a[j] > a[i]) g[i] = max(g[i], g[j] + 1);
int res = 0;
for (int i = 1; i <= n; i++)
{
if (i < n) res = max(res, f[i] + 1);
else res = max(res, f[i]);
if (i > 1 && a[i] != 0) res = max(res, g[i] + 1);
else res = max(res, g[i]);
for (int j = i + 2; j <= n; j++)
if (a[j] - a[i] > 1) res = max(res, f[i] + g[j] + 1);
}把数组划成 k 个区间,给定每个区间的权值,问 sigma(区间和*权值)最大值
显然 DP,核心是看最后一个数属于当前段还是新开一个段
f[i][j] = max(f[i - 1][j], f[i - 1][j - 1]) + a[i]*p[j]
摘樱桃
给
n × n网格,1代表樱桃,0代表空地,-1代表不能走,从左上到右下再回到左上,问最多经过几个有1的格子?
题意转换:看成是从左上到右下走两次,途径格子只能得分一次,等价于两个人同时从左上走,到右下角的最大得分
定义 f[k][i][j] 表示走了 k 步,第一个人在第 i 行,第二个人在第 j 行的最大得分。转移前驱有四个:分别是走行、走列。若当前位置不重叠,同时累加,否则累加一次。初始化为负无穷
f[2][1][1] = grid[0][0];
for (int k = 3; k <= 2 * n; k++)
for (int i1 = 1; i1 <= n; i1++)
for (int i2 = 1; i2 <= n; i2++) {
int j1 = k - i1, j2 = k - i2;
if (j1 <= 0 || j1 > n || j2 <= 0 || j2 > n) continue;
int A = grid[i1 - 1][j1 - 1], B = grid[i2 - 1][j2 - 1];
if (A == -1 || B == -1) continue;
int a = f[k - 1][i1 - 1][i2], b = f[k - 1][i1 - 1][i2 - 1];
int c = f[k - 1][i1][i2 - 1], d = f[k - 1][i1][i2];
int t = max(max(a, b), max(c, d)) + A;
if (i1 != i2) t += B;
f[k][i1][i2] = t;
}第一类斯特林数
第一类斯特林数指的是: 表示 个元素划分 个圆排列的方案数
LC1866 有
n根长度互不相同的木棍,长度为从1到n的整数。请你将这些木棍排成一排,并满足从左侧 可以看到 恰好k根木棍。从左侧 可以看到 木棍的前提是这个木棍的 左侧 不存在比它 更长的 木棍。
- 例如,如果木棍排列为
[1,3,2,5,4],那么从左侧可以看到的就是长度分别为1、3、5的木棍。- 给你
n和k,返回符合题目要求的排列 数目 。由于答案可能很大,请返回对10^(9)7取余的结果。 数据范围是1000
先看 DP 怎么做,定义 f[i][j] 表示考虑前 i 个数,有 j 个数被看到的方案数。转移时考虑最后一个数能否被看到:
- 能,那么最后一个数一定为
i,对应前i-1个数被看到j-1个数的方案数 - 不能,那么这个数可以是
x∈[1...i-1],然后我们排其它i-1个数,可以把[1...i]/x按相对大小映射到[1...i-1],也就相当于f[i-1][j],最后一共有i-1个数可作为最后一个
初始化 f[0][0]=1,其余都是 0
class Solution {
private:
static constexpr int mod = 1000000007;
public:
int rearrangeSticks(int n, int k) {
vector<int> f(k + 1);
f[0] = 1;
for (int i = 1; i <= n; ++i) {
vector<int> g(k + 1);
for (int j = 1; j <= k; ++j) {
g[j] = ((long long)f[j] * (i - 1) % mod + f[j - 1]) % mod;
}
f = move(g);
}
return f[k];
}
};转换为斯特林数:n 个数划分为 k 部分,每部分固定第一个数是被看到的,剩下的任意排列。假设长为 m,最大的数固定,一共 种,联系上圆排列了,那么答案就是 n 的排列划分成 k 个非空圆排列的方案数(代码同上面的)
第二类斯特林数
第二类斯特林数指的是: 表示 个不同的球分到 个相同的盒子的方案数,要求非空
代码
int S[N][N];
int cal(int N, int K) {
S[0][0] = 1;
for(int n = 1; n <= N; n ++)
for(int k = 1; k <= K; k++)
S[n][k] = (S[n - 1][k - 1] + (LL)k * S[n - 1][k] % md) % md;
return S[N][K];
}262144
P3147 给
n个数(2<=n<=262144),范围1-40,可以把两个相邻的相同数x合并成x+1,问最终得到的数最大是多少
区间 DP?但这个范围不行啊,而且这个范围也太奇怪了
秘密在于 262144=2^18,因此就算两两合并,最大能得到的数也只有 58
根据 58,考虑一下作为 DP 的维度
定义 f[i][j] 表示左端点是 j,能合并出 i 的右端点位置(注意是开区间,即 [j,f[i][j]) 合并出 i)
为什么这么定义?转移时就知道了,要想合成 i+1,先合成 i,那么此时 f[i][j] 就可以作为左端点了,f[i+1][j]=f[i][f[i][j]]!其实就是一个倍增的思想,但这个状态设计很特别
for (int i = 1; i <= n; i++) {
cin >> x;
f[x][i] = i + 1;
}
int res = 0;
for (int i = 2; i <= 58; i++) {
for (int j = 1; j <= n; j++) {
if (!f[i][j]) {
f[i][j] = f[i - 1][f[i - 1][j]];
}
if (f[i][j]) {
res = i;
}
}
}计数 DP
括号序列
给定括号字符串,添加最少括号使其变得合法,问方案数 两个结果是本质不同的是指存在某个位置一个结果是左括号,而另一个是右括号
合法序列对应性质:(1)左右括号数量相等;(2)任意前缀左括号数不小于右括号数。 此题的重要性质:左右括号都是添加到原括号序列的空隙中的,假如左括号和右括号加入的空隙不同,互不影响;假如相同,则一定先放完右括号再放左括号(否则形成一对新的匹配括号,可以删去),方式唯一确定。 怎么做题?现在原来的基础上算出只加左括号的方案数,然后将原序列逆序,并左右互变,再求一遍只加左括号的方案数(相当于原来序列只加右括号)。这个思路很难想出来,正确性看题解或举例说明。 f[i][j] 表示前 i 个字符中,左括号比右括号多 j 个的集合(j>=0),属性存方案数。 转移:规定遇到右括号才能加(避免重复)。遇到左括号:f[i][j]=f[i-1][j-1];遇到右括号:f[i][j] = f[i-1][0] + f[i-1][1] + … + f[i-1][j] + f[i-1][j+1]。 优化:利用类似多重背包的优化方法。 为什么答案是枚举 i?可以想成第一次算满足 左>=右,第二次算满足 右>=左,从小到大枚举到第一个非空集合就是取等的时候。 对为什么以右括号为分割点可以避免重复的解释:
单独考虑添加左括号,若以右括号为分割点, 将整个序列进行分割,因为分割后的子串中均为左括号, 添加任意数目的左括号方案数均为一种,那么此时,我们仅需考虑添加不同数量的左括号的方案数即可。
LL dp()
{
memset(f, 0, sizeof f);
f[0][0] = 1;
for (int i = 1; i <= n; i++)
if (str[i] == '(')
for (int j = 1; j <= n; j++)
f[i][j] = f[i - 1][j - 1];
else
{
f[i][0] = ((LL)f[i - 1][0] + f[i - 1][1]) % MOD;
for (int j = 1; j <= n; j++)
f[i][j] = ((LL)f[i][j - 1] + f[i - 1][j + 1]) % MOD;
}
for (int i = 0; i <= n; i++)
if (f[n][i]) return f[n][i];
return -1;
}
LL l = dp();
reverse(str + 1, str + n + 1);
for (int i = 1; i <= n; i++)
if (str[i] == '(') str[i] = ')';
else str[i] = '(';
LL r = dp();
printf("%d\n", l * r % MOD);活字印刷
你有一套活字字模
tiles,其中每个字模上都刻有一个字母tiles[i]。返回你可以印出的非空字母序列的数目。 **注意:**本题中,每个活字字模只能使用一次。
定义 f[i][j] 表示用前 i 种字符构造长为 j 的序列的方案数。集合划分:考虑第 i 种字符有 cnt 个
- 不选:
f[i][j] = f[i-1][j] - 枚举选
k个,从j个位置中选k个出来,其余位置为用i-1种字符构造j-k的方案数
const int N = 8;
int c[N][N];
class Solution {
public:
int numTilePossibilities(string tiles) {
for (int i = 0; i < N; i++)
for (int j = 0; j <= i; j++)
if (j == 0) c[i][j] = 1;
else c[i][j] = c[i - 1][j] + c[i - 1][j - 1];
unordered_map<char, int> cnt;
for (char c: tiles) cnt[c] ++;
int n = tiles.size(), m = cnt.size();
int f[m + 1][n + 1];
memset(f, 0, sizeof f);
f[0][0] = 1;
int i = 1;
for (auto &[_, t]: cnt) // 枚举第 i 个字符
{
for (int j = 0; j <= n; j++) // 枚举序列长度
for (int k = 0; k <= j && k <= t; k++) // 枚举选了几个
f[i][j] += f[i - 1][j - k] * c[j][k];
i ++;
}
return accumulate(f[m] + 1, f[m] + n + 1, 0);
}
};网格图上放积木
CF991D 输入一个 2 行 n(≤100) 列的棋盘。 用数字 0 表示空格子,大写字母 X 表示一开始就被占据的格子。 你有无数个 L 形状的积木,可以旋转,也就是如下 4 种形状: XX XX 0X X0 X0 0X XX XX 积木只能放在空格子上(占据 3 个空格子),不能放在被占据的格子上。积木之间不能重叠。 问:最多可以往棋盘上放多少个积木?
枚举到第 i 列时,看 i-1 列的情况进行转移,学习如何对摆放方式进行编码
int res = 0, pre = 0;
for (int i = 0; i < n; i++)
{
int cur = (s1[i] == '0') + (s2[i] == '0');
if (cur == 0) pre = 0;
if (cur == 1) pre == 2 ? (res ++, pre = 0) : pre = 1;
if (cur == 2) pre > 0 ? (res ++, pre = (pre == 2 ? 1 : 0)) : pre = 2;
}状压 DP
典中典:LCP 69. Hello LeetCode!
飞机降落
有
N架飞机准备降落到某个只有一条跑道的机场。 其中第i架飞机在Ti时刻到达机场上空,到达时它的剩余油料还可以继续盘旋Di个单位时间,即它最早可以于Ti时刻开始降落,最晚可以于Ti+Di时刻开始降落。 降落过程需要Li个单位时间。 一架飞机降落完毕时,另一架飞机可以立即在同一时刻开始降落,但是不能在前一架飞机完成降落前开始降落。 请你判断N架飞机是否可以全部安全降落。
注意到我们摆好一个集合后,我们不关心集合内部怎么摆的,只关心终点的最小值是多少。基于这个可以用状压 dp。状态计算对应一个集合的划分,我们可以把“f[i] 根据第 j 个为 1 的二进制位放在最右边”作为一个划分条件,就可以不重不漏划分了。 把 j 拿出来分析发现,只要除了它剩下的集合结束时间最靠前,那它也可以最靠前。依据此就可以写代码了。
memset(f, 0x3f, sizeof f); // 初始化
f[0] = 0;
for (int i = 1; i < 1 << n; i++)
for (int j = 0; j < n; j++)
{
int t = p[j].t, d = p[j].d, l = p[j].l;
if (i >> j & 1)
{
int last = f[i - (1 << j)];
if (t + d >= last)
f[i] = min(f[i], max(last, t) + l);
}
}二进制表示子集
门店商品调配 某连锁店开设了若干门店,门店间允许进行商品借调以应对暂时性的短缺。本月商品借调的情况记于数组
distributions,其中distributions[i] = [from,to,num],表示从from门店调配了num件商品给to门店。 若要使得每一个门店最终借出和借入的商品数量相同,请问至少还需要进行多少次商品调配。 **注意:**一次商品调配以三元组[from, to, num]表示,并有from ≠ to且num > 0。
假设拿一个二维坐标系,纵轴表示 cnt[i] ,借出表示正,借入表示负,就可以表示为一系列有正有负的矩形。 注意到借入借出平衡等价于 。然后如果某些矩形的 ,就成为了一个子问题,这就启发我们递归解决子问题。 定义 dp[i] 表示集合 i 通过调配后所有元素值均为 0 的方案,属性存储最少调配次数。由于数据范围很小,就可以考虑二进制表示子集。假设 i 的子集为 j ,那么补集就是 i^j ,如果 sum[j]=0 ,就可以转移。 dp[i] 的最大值是多少?极端情况下从一个大的值分给其它所有小的值,那么 dp[i] 就是集合 i 的大小减 1。 转移方程就是 dp[i]=min(dp[i], dp[j] + dp[i^j]) 。 如果 sum[i] != 0 ,不合法,令 dp[i] = INF 。 时间复杂度为 ,分析这个复杂度需要数学技巧,具体看 视频。
const int N = 12, M = 1 << 12;
class Solution {
public:
int minTransfers(vector<vector<int>>& distributions) {
int cnt[N] = {};
for (auto& d: distributions)
{
cnt[d[0]] -= d[2];
cnt[d[1]] += d[2];
}
int f[M] = {};
for (int i = 1; i < M; i++)
{
int sum = 0;
for (int j = 0; j < N; j++)
if (i >> j & 1) sum += cnt[j];
if (sum)
f[i] = INT_MAX / 2; // 元素和不为 0 非法
else
{
f[i] = __builtin_popcount(i) - 1; // 最大值
for (int j = (i - 1) & i; j; j = (j - 1) & i) // 枚举非空真子集
f[i] = min(f[i], f[j] + f[i ^ j]);
// 没有考虑 f[j] + f[i ^ j] 是否合法 因为不合法置成 INT_MAX / 2
// 既不会溢出 取 min 的时候也不会取到
}
}
return f[M - 1];
}
};暴搜代码
class Solution {
public:
int minTransfers(vector<vector<int>>& distributions) {
int cnt[12] = {};
for (auto& d: distributions)
{
cnt[d[0]] -= d[2];
cnt[d[1]] += d[2];
}
vector<int> a, b;
for (int x: cnt)
if (x > 0) a.push_back(x);
else if (x < 0) b.push_back(-x);
int res = 1e9;
function<void(int)> dfs = [&](int op)
{
if (op > res) return; // 剪枝
bool f = true;
for (int x: a) if (x) f = false;
if (f)
{
res = min(res, op);
return;
}
// 每次找出最小值 把它填补到另一个数组中
int mn = 1e9, t = 0, idx = 0;
for (int i = 0; i < a.size(); i++)
if (a[i] > 0 && a[i] < mn) mn = a[i], t = 0, idx = i;
for (int i = 0; i < b.size(); i++)
if (b[i] > 0 && b[i] < mn) mn = b[i], t = 1, idx = i;
if (t == 0)
{
a[idx] -= mn;
for (int i = 0; i < b.size(); i++)
if (b[i] > 0)
{
b[i] -= mn;
dfs(op + 1);
b[i] += mn;
}
a[idx] += mn;
}
else
{
b[idx] -= mn;
for (int i = 0; i < a.size(); i++)
if (a[i] > 0)
{
a[i] -= mn;
dfs(op + 1);
a[i] += mn;
}
b[idx] += mn;
}
};
dfs(0);
return res;
}
};最小必要团队
作为项目经理,你规划了一份需求的技能清单
req_skills,并打算从备选人员名单people中选出些人组成一个「必要团队」( 编号为i的备选人员people[i]含有一份该备选人员掌握的技能列表)。 所谓「必要团队」,就是在这个团队中,对于所需求的技能列表req_skills中列出的每项技能,团队中至少有一名成员已经掌握。可以用每个人的编号来表示团队中的成员:
- 例如,团队
team = [0, 1, 3]表示掌握技能分别为people[0],people[1],和people[3]的备选人员。 请你返回 任一 规模最小的必要团队,团队成员用人员编号表示。你可以按 任意顺序 返回答案,题目数据保证答案存在。
两种角度:
用人去更新状态:
class Solution {
public:
vector<int> smallestSufficientTeam(vector<string>& req_skills, vector<vector<string>>& people) {
int n = req_skills.size(), m = people.size();
unordered_map<string, int> idx;
for (int i = 0; i < n; i++) idx[req_skills[i]] = i;
vector<vector<int>> f(1 << n);
for (int i = 0; i < m; i++)
{
int cur = 0;
for (string& s: people[i]) cur |= (1 << idx[s]);
for (int pre = 0; pre < (1 << n); pre++)
{
if (pre > 0 && f[pre].empty()) continue;
int comb = pre | cur;
if (comb == pre) continue;
if (f[comb].empty() || f[pre].size() + 1 < f[comb].size())
{
f[comb] = f[pre];
f[comb].push_back(i);
}
}
}
return f[(1 << n) - 1];
}
};用状态去更新状态
class Solution {
public:
typedef long long LL;
vector<int> smallestSufficientTeam(vector<string>& req_skills, vector<vector<string>>& people) {
int m = req_skills.size();
unordered_map<string, int> idx;
for (int i = 0; i < m; i++) idx[req_skills[i]] = i;
int n = people.size(), mask[n];
memset(mask, 0, sizeof mask);
for (int i = 0; i < n; i++)
for (auto& s: people[i])
mask[i] |= (1 << idx[s]);
int u = 1 << m;
LL all = (1LL << n) - 1, f[u];
for (int i = 0; i < u; i++) f[i] = all;
f[0] = 0;
for (int j = 0; j < u - 1; j++) // f[u - 1] 无需计算
if (f[j] < all) // f[j] == all 说明这个状态还是初始值 即它还没被更新过
for (int i = 0; i < n; i++)
if (__builtin_popcountll(f[j]) + 1 < __builtin_popcountll(f[j | mask[i]]))
f[j | mask[i]] = f[j] | (1LL << i);
LL ans = f[u - 1];
vector<int> res;
for (int i = 0; i < n; i++)
if ((ans >> i) & 1) res.push_back(i);
return res;
}
};排列型状压 DP
给数组
a和b,固定a,b可以任意排列,求a和b对应项异或值之和的最小值
通过状压 DP 把枚举全排列的复杂度降至
设 mask 表示选了 b 中哪些数,假设 mask 中有 s 个 1,然后枚举 mask 中哪个数与 a[s-1] 进行匹配
for (int i = 1; i < 1 << n; i++)
{
int s = __builtin_popcount(i);
for (int j = 0; j < n; j++)
if (i >> j & 1)
f[i] = min(f[i], f[i - (1 << j)] + (nums1[s - 1] ^ nums2[j]));
}P1357 花园(环形、矩阵)
环形的数组,元素要么是
C要么是P,要求相邻m个元素中,C不超过k个n为1e15,m,k<5
用状压表示相邻
m个的状态,有1<<m个转移方程,当前为
i- 滑出窗口的是 0,那么上个状态就是
i>>1 - 滑出窗口的是 1,上个状态就是
(i>>1)|(1<<(m-1)),当然,需要判断这个状态是否合法
- 滑出窗口的是 0,那么上个状态就是
**(重点)**环的处理:由于花园是环形的,所以
1~m号花圃会对n-m+2~n号花圃产生影响。为了确定产生的到底是什么样的影响,我们就需要枚举1~m号花圃的状态,对每种状态进行一次递推。设1~m号花圃的状态为s,则最终答案就是f(n+m,s)转移矩阵怎么构造:根据转移方程来,如果
i->j,那么a[i][j]=1,这个很实用!细节:原来是要枚举初始状态嘛,现在用矩阵,就令
f[0][0]=f[1][1]=...=1,这个就是个单位矩阵,f*a还是等于a,那么最后只需要累加a[i][i]就是答案了
int res = 0;
// n 在 1e5 时的做法
// for (int st = 0; st < 1 << m; st++) {
// if (__builtin_popcount(st) > k) {
// continue;
// }
// memset(f, 0, sizeof(f));
// f[0][st] = 1;
// for (int i = 1; i <= n; i++) {
// for (int j = 0; j < 1 << m; j++) {
// f[i][j] = f[i - 1][j >> 1];
// int last = (j >> 1) | (1 << (m - 1));
// if (__builtin_popcount(last) <= k) {
// f[i][j] = (f[i][j] + f[i - 1][last]) % MOD;
// }
// }
// }
// res = (res + f[n][st]) % MOD;
// }
// cout << res << endl;
vector<vector<int>> a(1 << m, vector<int>(1 << m));
for (int i = 0; i < 1 << m; i++) {
if (__builtin_popcount(i) > k) {
continue;
}
int j = i >> 1;
a[j][i] = 1; // j -> i
j = (i >> 1) | (1 << (m - 1));
if (__builtin_popcount(j) <= k) {
a[j][i] = 1; // j -> i
}
}
auto ans = qmi(a, n);
for (int i = 0; i < 1 << m; i++) {
res = (res + ans[i][i]) % MOD;
}
cout << res << endl;统计无向图中的简单环
CF11D 求无向图中的简单环个数,保证不存在重边和自环。 简单环:除起点外,其余的点都只出现一次的回路。 点数最多是
19
数据范围小-> 没有多项式时间解法
设计 f[k][i] 表示当前考虑的点集为 k,当前点为 i 时,起点到 i 的简单路径数。为了不重复统计,人为规定起点是 k 中编号最小的点。枚举 i 的邻居 j
- 如果是起点,构成环
- 如果编号小于起点,不合法
- 否则,路径数从
i转移到j
细节:这种算法重复统计了
- 所有的
a-b边都被算成环,想想点集只有两个元素时的情况 - 所有简单环都被统计了两次,想想固定
k时,从s-i-j的路径被记录,但是从j-i-s的路径也会被记录
for (int i = 0; i < n; i++) {
f[1 << i][i] = 1;
}
for (int k = 1; k < 1 << n; k++) {
for (int i = 0; i < n; i++) {
if (f[k][i] == 0) {
continue;
}
for (int j = 0; j < n; j++) {
if (!g[i][j] || (k & -k) > (1 << j)) {
continue; // 不连通或者小于起点
}
if (k & 1 << j) { // 这个点在点集内
if ((k & -k) == (1 << j)) { // 如果是起点
res += f[k][i];
}
} else {
f[k | (1 << j)][j] += f[k][i]; // 路径数转移
}
}
}
}
cout << (res - m) / 2 << endl;偶像出列!
P3694 有
n个偶像来自m个乐队,要求重新排列,使得同一乐队的站到一起。方式是,让一部分人出列,然后任意插回到空位中,问最少出列几人n的范围是1e5,m的范围是20
不难,积累下思路

DP + 构造
最短公共超序列
给你两个字符串
str1和str2,返回同时以str1和str2作为 子序列 的最短字符串。如果答案不止一个,则可以返回满足条件的 任意一个 答案。 如果从字符串t中删除一些字符(也可能不删除),可以得到字符串s,那么s就是t的一个子序列。
预处理出 LCS 数组后,用双指针来构造
- 如果
ij其一走完,那么剩余字符加到答案中 f[i][j] = f[i-1][j-1]且s[i]=t[j]时,ij同时后移- 否则就看移
i还是j,或者任取其一
class Solution {
public:
string shortestCommonSupersequence(string s, string t) {
int n = s.size(), m = t.size(), f[n + 1][m + 1];
memset(f, 0, sizeof f);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
if (s[i - 1] == t[j - 1]) f[i][j] = f[i - 1][j - 1] + 1;
else f[i][j] = max(f[i - 1][j], f[i][j - 1]);
string res;
int i = n, j = m;
s = " " + s, t = " " + t;
while (i > 0 || j > 0)
{
if (i == 0) res += t[j --];
else if (j == 0) res += s[i --];
else
{
if (s[i] == t[j])
{
res += s[i];
i --, j --;
}
else if (f[i][j] == f[i - 1][j]) // 思考下为什么
res += s[i --];
else res += t[j --];
}
}
reverse(res.begin(), res.end());
return res;
}
};状态机 DP
问长为 n 的串,含有 l e e t,问方案数
维护 f(i,l,e,t) 表示长为 i,至少含 i 个 i,e 个 e,t 个 t 的方案数,转移方程为
// 下一个字符填写除了 l, e, t 以外的 23 个字母
f(i + 1, l, e, t) += f(i, l, e, t) * 23;
// 下一个字符填写 l
// 这里用 min 限制 l 的范围是因为只要有至少一个 l 就是好字符串,我们不关心具体有几个 l
f(i + 1, min(1, l + 1), e, t) += f(i, l, e, t);
// 下一个字符填写 e
f(i + 1, l, min(2, e + 1), t) += f(i, l, e, t);
// 下一个字符填写 t
f(i + 1, l, e, min(1, t + 1)) += f(i, l, e, t);答案为
class Solution {
public:
int stringCount(int n) {
LL f[n + 1][2][3][2];
memset(f, 0, sizeof f);
f[0][0][0][0] = 1;
for (int i = 0; i < n; i++)
for (int j = 0; j < 2; j++)
for (int k = 0; k < 3; k++)
for (int l = 0; l < 2; l++)
{
f[i + 1][j][k][l] = (f[i + 1][j][k][l] + f[i][j][k][l] * 23) % MOD;
f[i + 1][min(j + 1, 1)][k][l] = (f[i + 1][min(j + 1, 1)][k][l] + f[i][j][k][l]) % MOD;
f[i + 1][j][min(k + 1, 2)][l] = (f[i + 1][j][min(k + 1, 2)][l] + f[i][j][k][l]) % MOD;
f[i + 1][j][k][min(l + 1, 1)] = (f[i + 1][j][k][min(l + 1, 1)] + f[i][j][k][l]) % MOD;
}
return f[n][1][2][1];
}
};基于状态机的 7 进制状压
LCP76 棋盘上有空格、黑棋、红棋和问号四种,问号可以填入前三种,不产生冲突的填法有多少种(
n*m<=30) 产生冲突的定义:两颗不同颜色的棋子,在同一行或同一列;且之间恰好有一颗棋子(可以有空位)
从简单的情况入手,只有一行,且没有空格子,怎么填?关键的观察:当前能不能放取决于最后两个棋子的状态,因此可以归纳出 7 种状态:
- X,表示空,可放 R 或 B
- R,只有一个 R,此时可放 R 或 B,形成 RR 或 RB
- B,同理形成 BB 或 BR
- RR,只能放 R
- BB,只能放 B
- RB,只能放 R
- BR,只能放 B
状态迁移就可以用状态机来表示,接下来考虑怎么 DP
用 f[i][j][col_states][row_state] 表示当前正在考虑第 i 行第 j 列,所有列的状态表示为 col_states,是 7 进制数,当前行的状态为 row_state
每次更新时基于当前状态和状态机去更新
具体来说,分析得到 min(n,m)<=5,如果 n<m,就把 n 和 m 互换。然后枚举每一个位置,对每一个位置,都枚举 col_states 和 row_state,把 col_states 中当前列的信息取出来,枚举这一个格子填什么,并判断是否可以填这个,如果可以,计算新的行列状态,然后更新 f[ni][nj]。这里如果 nj 超过边界,就跳到下一行的第 0 个位置,这样最后计算答案时就考虑 f[n][0] 即可
class Solution {
public:
long long getSchemeCount(int n, int m, vector<string>& a) {
if (n < m) {
vector<string> b(m);
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++) b[j].push_back(a[i][j]);
a = std::move(b);
swap(n, m);
}
int X = 0, R = 1, B = 2, R2 = 3, B2 = 4, RB = 5, BR = 6;
int g[7][7];
memset(g, -1, sizeof g);
for (int i = 0; i < 7; i++) g[i][0] = i; // 放空格
g[X][R] = R;
g[X][B] = B;
g[R][R] = R2;
g[B][B] = B2;
g[R][B] = RB;
g[B][R] = BR;
g[R2][R] = R2;
g[B2][B] = B2;
g[RB][R] = BR;
g[BR][B] = RB;
int tot = 1;
for (int i = 0; i < m; i++) tot *= 7;
LL f[n + 1][m + 1][tot][7];
memset(f, 0, sizeof f);
f[0][0][0][0] = 1;
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++) {
int cur = -1;
if (a[i][j] == 'R') cur = R;
if (a[i][j] == 'B') cur = B;
if (a[i][j] == '.') cur = X;
// 当前状态更新往右一格(如果达到边界就进入下一行)
int ni = i, nj = j + 1;
if (nj == m) ni ++, nj = 0;
int base = 1;
for (int k = 0; k < j; k++) base *= 7;
for (int col_sts = 0; col_sts < tot; col_sts++) {
int col_st = col_sts / base % 7;
for (int row_st = 0; row_st < 7; row_st++) {
for (int nxt = 0; nxt < 3; nxt++)
if (cur == -1 || cur == nxt)
if (g[col_st][nxt] != -1 && g[row_st][nxt] != -1) {
int new_col_st = col_sts + (g[col_st][nxt] - col_st) * base;
int new_row_st = g[row_st][nxt];
if (ni != i) new_row_st = 0;
f[ni][nj][new_col_st][new_row_st] += f[i][j][col_st][row_st];
}
}
}
}
LL res = 0;
for (int col_st = 0; col_st < tot; col_st++)
res += f[n][0][col_st][0];
return res;
}
};SOS-DP
求 a[i]+a[j]=a[i]^a[j] 的数对数
可以想到,当前位为 0 的话,对应位置可以是 0 或 1;当前位为 1 的话,对应位置只能是 0
反转一下,把这一位为 0 的加到为 1 的统计值中,最后求 a[i] 对应的数对时,把 a[i] 异或 mask 反转一下
这个做法实际上叫做 高维前缀和(SOSDP),一般用于子集求和类问题,当然它不止可以求前缀和,前缀积,前缀 max,前缀 min 都可以。这篇博客介绍得很清楚
// S(mask,i) 表示 mask 子集中只有最右边 i 位与其不同的状态
// 从博客的树状图可以很容易理解这个 dp 的过程
for(int i=0;i<w;++i)//依次枚举每个维度(从右边数起第几位)
{
for(int j=0;j<(1<<w);++j)//求每个维度的前缀和
{
if(j&(1<<i))s[j]+=s[j^(1<<i)];
}
}for (int i = 0; i < 20; i++)
for (int j = 0; j < 1 << 20; j++)
if (j >> i & 1) sum[j] += sum[j ^ (1 << i)];
int msk = (1 << 20) - 1;
LL res = 0;
for (int i = 1; i <= n; i++) res += sum[a[i] ^ msk];两道 SOS-DP 的经典题

PII merge(PII s, PII t)
{
if (s.x < t.x) swap(s, t);
PII res = s;
if (t.x > res.y) res.y = t.x;
return res;
}
cin >> n;
for (int i = 0; i < 1 << n; i++)
{
cin >> x;
a[i] = {x, -INF};
}
for (int j = 0; j < n; j++)
for (int i = 0; i < 1 << n; i++)
if (i >> j & 1) a[i] = merge(a[i], a[i ^ (1 << j)]);
int res = 0;
for (int i = 1; i < 1 << n; i++)
{
res = max(res, a[i].x + a[i].y);
cout << res << endl;
}
void add(int v, int id)
{
if (f[v].x == id || f[v].y == id) return;
if (f[v].x == -1) f[v].x = id;
else if (f[v].y == -1)
{
f[v].y = id;
if (f[v].x < f[v].y) swap(f[v].x, f[v].y);
}
else if (f[v].x < id)
{
f[v].y = f[v].x;
f[v].x = id;
}
else if (f[v].y < id) f[v].y = id;
}
void merge(int A, int B)
{
add(A, f[B].x);
add(A, f[B].y);
}
memset(f, -1, sizeof f);
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
add(a[i], i);
}
for (int i = 0; i < 21; i++)
for (int j = 0; j < N; j++)
if (j >> i & 1) merge(j ^ (1 << i), j); // 超集的做法和子集反过来
int res = 0;
for (int i = 1; i <= n - 2; i++)
{
int msk = (1 << 21) - 1;
int cur = a[i] ^ msk, mx = 0;
for (int j = 20; j >= 0; j--)
if (cur >> j & 1 && f[mx ^ (1 << j)].y > i)
// 看是否存在两个大于 i 的位置 它们 & 的结果为当前答案的超集
mx |= 1 << j;
res = max(res, mx | a[i]);
}
cout << res << endl;茶中 DP
数组划分为 k 段的最大的分
https://codeforces.com/problemset/problem/833/B 输入 n(1≤n≤35000) k(1≤k≤min(50,n)) 和长为 n 的数组 a(1≤a[i]≤n)。 你需要把 a 划分成 k 个非空连续段。 每段的得分 = 这一段的不同元素个数。 输出这 k 段的得分之和的最大值。
提示 1
先把这题做了 字符串的总引力
提示 2
本题是划分型 DP,定义 f[k][i] 表示把前 i 个数分成 k 段的最大得分。
枚举第 k 段的开始位置 j,那么 f[k][i] = max{f[k-1][j-1] + 从 j 到 i 的不同元素个数}
提示 3
在枚举 i 的同时,用 lazy 线段树维护如下序列的区间最大值(维护转移来源的最大值):
序列的位置 L 维护着从 L 到 i 的不同元素个数,再加上 f[k-1][L-1]。这里的【加上 f[k-1][L-1]】在初始化线段树的时候完成。
遍历到 a[i] 时,把序列的下标 [pre+1,i] 内的数都 +1,这里 pre 是 a[i] 上一次出现的下标。
这样 f[k][i] 就等于线段树的 query(1,i) 了。
答疑:题目要求子数组不能为空,为什么可以直接 query(1,i)?不应该给前面的子段留下一些位置吗?
解答:没关系,分出来的子段越多,f 必然越大,query(1,i) 一定会取到分出 k 段的答案。
代码实现时,f 的第一个维度可以去掉,只需要一棵线段树。
启发:希望在 logn 的时间内可以求出 [i,j] 的不同颜色个数,考虑它上一次出现的位置 pre[i],就要给 [pre[i]+1,i] 都加上 1,这个区间加的操作就可以用线段树完成。难点在于需要建树 k 次,每次记录上次的 f 值
cin >> n >> k;
for (int i = 1; i <= n; i++)
{
cin >> v;
pre[i] = p[v];
p[v] = i;
}
while (k -- )
{
build(1, 1, n);
for (int i = 1; i <= n; i++)
{
update(1, pre[i] + 1, i, 1);
f[i] = query(1, 1, i);
}
}
cout << f[n] << endl;图上 DP 新奇的维度设计
https://codeforces.com/contest/721/problem/C 输入 n(2≤n≤5000) m(1≤m≤5000) maxT(1≤maxT≤1e9)。 然后输入 m 条边,每条边输入 v w t(1≤wt≤1e9),表示有一条边权为 t 的有向边连接 v 和 w。节点编号从 1 开始。 保证输入的是一个有向无环图,并且没有重边。 求出从 1 到 n 的一条路径,要求路径长度(边权之和)不超过 maxT,在满足该条件的前提下,路径上的节点数最多。 输出两行,第一行是路径上的节点个数,第二行按顺序输出路径上的节点编号(第一个数必须是 1,最后一个数必须是 n)。 保证至少有一条满足要求的路径。
无需建图的 DP
提示 1:把「经过了多少个点」作为额外的 DP 维度,把「最短长度」作为 DP 值。
提示 2:定义 f[i][w] 表示从 1 到 w,经过了 i+1 个点的最短长度。i 最大为 n-1。
初始值:f[0][1] = 0,其余为无穷大。
状态转移方程:f[i][w] = min(f[i-1][v]+t),其中有向边 v->w 的边权为 t。
答案:最大的满足 f[i][n] <= maxT 的 i,再加一(注意 i 是从 0 开始的)。
提示 3:从转移方程可以看出,其实不需要建图,只需要循环 n-1 次,每次遍历这 m 条边,在遍历时计算状态转移。
这是因为 f[i][] 只依赖于 f[i-1][],在把 f[i-1][] 算出来后,无论按照什么顺序遍历这 m 条边都是可以的。
提示 4:计算状态转移的时候,额外记录转移来源 from[i][w] = v。
从 n 出发,顺着 from 数组回到 1,就得到了具体方案。具体请看代码。
cin >> n >> m >> T;
for (int i = 0; i < m; i++)
cin >> es[i][0] >> es[i][1] >> es[i][2];
for (int i = 0; i < n; i++)
for (int j = 1; j <= n; j++)
f[i][j] = T + 1;
f[0][1] = 0;
int res = 0;
for (int i = 1; i < n; i++)
{
for (int j = 0; j < m; j++)
{
int v = es[j][0], w = es[j][1], t = es[j][2];
if (f[i - 1][v] + t < f[i][w])
{
f[i][w] = f[i - 1][v] + t;
from[i][w] = v;
}
}
if (f[i][n] <= T) res = i;
}
cout << res + 1 << endl;
int v = n;
for (int i = res; i >= 0; i--)
{
path[i] = v;
v = from[i][v];
}
for (int i = 0; i <= res; i++)
cout << path[i] << ' ';线性 DP 求方案数
https://codeforces.com/contest/404/problem/D 输入一个长度在 [1,1e6] 内的字符串,由五种字符 *?012 组成,表示一个「一维扫雷游戏」的局面。 其中 * 表示雷,数字表示左右相邻位置有多少个雷。 把 ? 替换成 *012 中的一个,可以得到多少个合法的局面?模 1e9+7。
状态比较多的线性 DP,自己做出来了,用了一个小时
初版是设置了 6 个状态,而后发现 1 和 3 可以合为一种情况,即“11”可以归到“01”这种情况中,不影响后面的计算(用有雷、没雷去思考似乎更好,就不用从字符是什么来思考)
当然,可以采用滚动数组优化
题解的代码太简洁了,有点难看懂,而且自己很难想出来,就不看了
/* origin
0: 0
1: 01
2: *1
3: 11
4: 2
5: *
*/
/* new
0: 0
1: 01
2: *1
3: 2
4: *
*/
int main()
{
cin >> s;
int n = s.size();
switch (s[0]) {
case '0': f[0][0] = 1; break;
case '1': f[0][1] = 1; break; // 不能写成 f[0][1] = f[0][3] = 1
case '2': break;
case '?': f[0][0] = f[0][1] = f[0][5] = 1; break;
case '*': f[0][5] = 1; break;
}
for (int i = 1; i < n; i++)
{
char c = s[i];
if (c == '0' || c == '?') f[i][0] = (f[i - 1][0] + f[i - 1][2]) % MOD;
if (c == '1' || c == '?')
{
f[i][1] = f[i - 1][0];
f[i][2] = f[i - 1][5];
f[i][3] = f[i - 1][2];
}
if (c == '2' || c == '?') f[i][4] = f[i - 1][5];
if (c == '*' || c == '?') f[i][5] = (f[i - 1][1] + f[i - 1][3] + f[i - 1][4] + f[i - 1][5]) % MOD;
}
LL res = (f[n - 1][0] + f[n - 1][2] + f[n - 1][5]) % MOD;
printf("%lld\n", res);
return 0;
}
// new
int main()
{
cin >> s;
int n = s.size();
switch (s[0]) {
case '0': f[0][0] = 1; break;
case '1': f[0][1] = 1; break;
case '2': break;
case '?': f[0][0] = f[0][1] = f[0][4] = 1; break;
case '*': f[0][4] = 1; break;
}
for (int i = 1; i < n; i++)
{
char c = s[i];
if (c == '0' || c == '?') f[i][0] = (f[i - 1][0] + f[i - 1][2]) % MOD;
if (c == '1' || c == '?')
{
f[i][1] = (f[i - 1][0] + f[i - 1][2]) % MOD;
f[i][2] = f[i - 1][4];
}
if (c == '2' || c == '?') f[i][3] = f[i - 1][4];
if (c == '*' || c == '?') f[i][4] = (f[i - 1][1] + f[i - 1][3] + f[i - 1][4]) % MOD;
}
LL res = (f[n - 1][0] + f[n - 1][2] + f[n - 1][4]) % MOD;
printf("%lld\n", res);
return 0;
}单调队列优化 DP
https://codeforces.com/problemset/problem/487/B 输入 n(1≤n≤1e5) s(0≤n≤1e9) L(1≤n≤1e5) 和长为 n 的数组 a(-1e9≤a[i]≤1e9)。 你需要把 a 分割成若干段(连续子数组),满足:
- 每段长度至少为 L。
- 每段的最大值减最小值 <= s。 输出至少要把 a 分成多少段。 如果无法做到,输出 -1。
考虑 DP,当子数组右端点固定时,左端点的最小值也是固定的。假如 [j,i] 的极差超过了 s,那么 [j-1,i] 的极差一定也超过 s,只需要维护一个决策点 c,如果 c 越大,f_c 不会变小,因此找到最小的合法 c 即可
如何优化求极差:i 和 c 都单增,考虑用单调队列来优化,当发现 最大值-最小值 >s 时就移动窗口
int n, s, l, c; // 决策点 c
int f[N], a[N];
deque<int> mn, mx;
int query()
{
while (mn.size() && mn.front() <= c) mn.pop_front();
while (mx.size() && mx.front() <= c) mx.pop_front();
return a[mx.front()] - a[mn.front()];
}
int main()
{
scanf("%d%d%d", &n, &s, &l);
for (int i = 1; i <= n; i++)
{
scanf("%d", &a[i]);
f[i] = INF;
}
for (int i = 1; i <= n; i++)
{
while (mn.size() && a[i] < a[mn.back()]) mn.pop_back();
mn.push_back(i);
while (mx.size() && a[i] > a[mx.back()]) mx.pop_back();
mx.push_back(i);
if (i >= l)
{
// 合法的 c 所以还要判断 f[c] == INF
while (i - c >= l && (query() > s || f[c] == INF)) c ++;
if (i - c >= l) f[i] = f[c] + 1;
}
}
printf("%d\n", f[n] >= INF ? -1 : f[n]);
return 0;
}DP + 构造
https://atcoder.jp/contests/abc222/tasks/abc222_d 输入 n(1≤n≤3000) 和两个长为 n 的数组 a b,元素范围在 [0,3000],且均为递增数组(允许有相同元素)。 构造递增数组 c(允许有相同元素),满足 a[i]<=c[i]<=b[i]。 输出你能构造多少个不同的 c,模 998244353。
有两种定义 DP 的方式。
定义 f[i][j] 表示考虑前 i 个数,其中第 i 个数填 j 的方案数
那么有 f[i][j] = f[i-1][0] + f[i-1][1] + ... + f[i-1][min(j, b[i-1])]
这可以用前缀和优化。
这启发我们,也可以直接定义 f[i][j] 表示考虑前 i 个数,其中第 i 个数填的数 <=j 的方案数。
考虑第 i 个数是否要填 j:
- 不填,那就是第 i 个数填的数 <=j-1 的方案数,即 f[i][j] = f[i][j-1]。
- 填,那么第 i-1 个数至多为 j,即 f[i][j] = f[i-1][min(j, b[i-1])]。
则有 f[i][j] = f[i][j-1] + f[i-1][min(j, b[i-1])]。
初始值 f[0][j] = j-a[0]+1,其中 a[0]<=j<=b[0]。
答案为 f[n-1][b[n-1]]。
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i++) scanf("%d", &a[i]);
for (int i = 0; i < n; i++) scanf("%d", &b[i]);
for (int j = a[0]; j <= b[0]; j++)
f[0][j] = j - a[0] + 1;
for (int i = 1; i < n; i++)
for (int j = a[i]; j <= b[i]; j++)
// 注意不要越界
f[i][j] = (f[i][max(j - 1, 0)] + f[i - 1][min(j, b[i - 1])]) % mod;
printf("%lld\n", f[n - 1][b[n - 1]]);
return 0;
}延迟 DP
https://atcoder.jp/contests/diverta2019/tasks/diverta2019_e 输入 n(1≤n≤5e5) 和长为 n 的数组 a(0≤a[i]<2^20)。 把数组 a 划分成若干段连续子数组,一共有 2^(n-1) 种划分方案。 问:其中有多少种划分方案,可以让每段子数组的异或和都一样? 答案模 1e9+7。
一眼 DP ,思考方向是计算前缀异或和数组,然后假设选定一些划分位置,异或和相同等价于 s[0]^s[i0]=s[i0]^s[i1]=...=s[im]^s[n] ,接着观察出 s[0]=s[i1]=... 以及 s[i0]=s[i2]=... 这个性质,那么转换为在前缀和数组中选择一个交替子序列,第一个数和最后一个数必选。
难点在于讨论 s[n] 的情况,对应如何转移,以及 延迟 DP ,代码上学习 struct f[] 的作用:统一两种情况的计算
struct {
int s0 = 1;
int s1, pre0;
} f[1 << 20];
int n, v, sum;
int qmi(int a, int k)
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % MOD;
a = (LL)a * a % MOD;
k >>= 1;
}
return res;
}
int main()
{
int cnt0 = 1;
scanf("%d", &n);
for (int i = 0; i < n; i++)
{
scanf("%d", &v);
sum ^= v;
if (sum == 0) cnt0 ++;
else
{
auto &t = f[sum];
// 延迟计算两个 非零数 之间 0 的个数对应的转移
t.s0 = (t.s0 + (LL)t.s1 * (cnt0 - t.pre0) % MOD) % MOD;
t.s1 = (t.s0 + t.s1) % MOD;
t.pre0 = cnt0;
}
}
if (sum > 0) printf("%d\n", f[sum].s0);
else
{
int res = qmi(2, cnt0 - 2);
for (int i = 0; i < 1 << 20; i++)
// res = f[n][0] + sum(f[j][1])
res = (res + f[i].s1) % MOD;
printf("%d\n", res);
}
return 0;
}十进制 SOS DP
https://atcoder.jp/contests/arc136/tasks/arc136_d 输入 n(2≤n≤1e6) 和长为 n 的数组 a(0≤a[i]<1e6)。 输出满足【十进制加法 a[i]+a[j] 的每个数位都没有产生进位】的下标对 (i,j) 个数,其中 i<j。
举例,如果一个数和 666 相加不进位,那么与 665 相加也不会进位。
定义 y 是 x 的「十进制子集」,当且仅当 y 的所有数位都小于等于 x 对应的数位。例如 666,566,656,665,123,66 都是 666 的十进制子集。
定义 f[i] 表示 i 的十进制子集的个数。
为什么要这样定义?对于 a[i] 来说,999999-a[i] 的任意十进制子集与 a[i] 相加都不会进位,所以 f[999999-a[i]] 就是与 a[i] 相加不进位的数字个数。
枚举 i 的第 j 个数位,如果这个数位大于 0,那么
f[i] += f[i-pow(10,j)]
初始值:f[x] = x 在数组 a 中的出现次数。
然后遍历 a[i],把 f[999999-a[i]] 加到答案中。
如果 a[i]+a[i] 没有进位,那么我们多统计了一个答案,ans--。
最后把答案除以 2,因为 (a[i],a[j]) 和 (a[j],a[i]) 我们都统计了一次。
注:如果你之前学过二进制的 SOS DP,对于想出本题做法有帮助。
本题相当于是十进制的 SOS DP。
代码中先枚举数位再枚举每个数的目的是
保证任意两个数之间只有一条路径,避免重复计算 例如:111 -> 112 -> 122 -> 222 低位累加在高位累加之前 而不会通过 111 -> 121 -> 221 -> 222 高低位混合累加 路径不唯一
也可以理解成从固定左边,最右边第一位可变化;最右边两位可变化 ...
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i++)
{
scanf("%d", &a[i]);
f[a[i]] ++;
}
for (int i = 1; i < 1e6; i *= 10)
for (int j = 0; j < 1e6; j++)
if (j / i % 10 > 0)
f[j] += f[j - i];
LL res = 0;
for (int i = 0; i < n; i++)
{
res += f[999999 - a[i]];
bool t = true;
for (int j = 1; j < 1e6; j *= 10)
if (a[i] / j % 10 >= 5) t = false;
if (t) res --;
}
printf("%lld\n", res / 2);
return 0;
}基础 DP 但要优化空间
https://atcoder.jp/contests/abc248/tasks/abc248_c 输入 n m(1≤n,m≤50) k(n≤k≤n*m)。 输出有多少个长为 n 的数组 a 满足 1≤a[i]≤m 且 sum(a)≤k。 模 998244353。
f[i][j] 表示前 i 个数的元素和为 j 的方案数。i 从 1 开始。
f[i][j] = f[i-1][j-1] + f[i-1][j-2] + ... + f[i-1][max(j-m,0)]
初始值 f[0][0] = 1。
答案为 sum(f[n])。
这种 DP 的空间优化版本不太会写
int main()
{
int n, m, k;
cin >> n >> m >> k;
int f[k + 1];
memset(f, 0, sizeof f);
f[0] = 1;
for (int i = n; i; i--)
for (int j = k; j >= 0; j--)
{
f[j] = 0;
for (int v = 1; v <= m && v <= j; v++)
f[j] = (f[j] + f[j - v]) % mod;
}
LL res = 0;
for (int i = 0; i <= k; i++) res = (res + f[i]) % mod;
cout << res << endl;
}TSP 问题
https://atcoder.jp/contests/abc301/tasks/abc301_e 输入 n m(1≤n,m≤300) t(1≤t≤2e6) 和一个 n 行 m 列的网格图。 S 为起点(恰好一个)。 G 为终点(恰好一个)。 . 为空地。
#为墙壁。o 为糖果(至多 18 个)。 你需要从起点走到终点。每一步可以上下左右四个方向走到相邻的非墙壁格子上,不能出界。 你可以重复访问同一个格子。 注:如果走到终点,可以继续走,只要最后在终点就行。 至多走 t 步。 输出你至多能收集多少个糖果(走到 o 即可收集,同一个格子只能收集一次)。 如果无法在 t 步内到达终点,输出 -1。 相似题目: LCP 13. 寻宝
计算每对 o 之间的最短距离,用 dis 数组记录。这一步可以用 BFS 解决。
由于 o 至多有 18 个,可以转换成一个旅行商问题(请自行搜索),用状压 DP 解决。
定义 f[s][i] 表示已收集的 o 的下标集合为 s,且当前在第 i 个 o 时的最小移动步数。
枚举 s 的补集中的下标 j,用 f[s][i] + dis[i][j] 去更新 f[s|1<<j][j] 的最小值。
时间复杂度 O(knm+k^2*2^k)。
本题学习如何记录最短距离,如何用状压 DP 解 TSP 问题
int n, m, t, sx, sy, tx, ty;
vector<PII> ps;
char c[310][310];
int d[20][310][310];
int main()
{
scanf("%d%d%d", &n, &m, &t);
for (int i = 0; i < n; i++)
{
scanf("%s", c[i]);
for (int j = 0; j < m; j++)
if (c[i][j] == 'S') sx = i, sy = j;
else if (c[i][j] == 'G') tx = i, ty = j;
else if (c[i][j] == 'o') ps.push_back({i, j});
}
ps.push_back({sx, sy});
int cnt = ps.size();
for (int i = 0; i < cnt; i++)
{
memset(d[i], 0x3f, sizeof d[i]);
int si = ps[i].x, sj = ps[i].y;
queue<PII> q;
d[i][si][sj] = 0;
q.push({si, sj});
while (q.size())
{
int x = q.front().x, y = q.front().y;
q.pop();
for (int k = 0; k < 4; k++)
{
int a = x + dx[k], b = y + dy[k];
if (a < 0 || a >= n || b < 0 || b >= m || c[a][b] == '#') continue;
if (d[i][a][b] > d[i][x][y] + 1)
{
d[i][a][b] = d[i][x][y] + 1;
q.push({a, b});
}
}
}
}
cnt --;
int f[1 << cnt][cnt];
memset(f, 0x3f, sizeof f);
for (int i = 0; i < cnt; i++) f[1 << i][i] = d[i][sx][sy];
for (int s = 1; s < 1 << cnt; s++)
{
for (int last = 0; last < cnt; last++)
{
if (f[s][last] == inf) continue;
for (int nx = 0; nx < cnt; nx++)
if ((s >> nx & 1) == 0)
if (f[s | (1 << nx)][nx] > f[s][last] + d[last][ps[nx].x][ps[nx].y])
f[s | (1 << nx)][nx] = f[s][last] + d[last][ps[nx].x][ps[nx].y];
}
}
int res = -1;
if (d[cnt][tx][ty] <= t) res = 0;
for (int s = 1; s < 1 << cnt; s++)
for (int last = 0; last < cnt; last++)
if (f[s][last] + d[last][tx][ty] <= t)
{
int ans = 0;
for (int i = 0; i < cnt; i++)
if (s >> i & 1) ans ++;
res = max(res, ans);
}
printf("%d\n", res);
return 0;
}另附 LCP.13 的代码,非常相像
class Solution {
public:
int n, m;
bool valid(int x, int y){
return x >= 0 && x < n && y >= 0 && y < m;
}
vector<vector<int>> bfs(int x, int y, vector<string>& maze){
// 板
vector<vector<int>> res(n, vector<int>(m, -1));
res[x][y] = 0;
queue<PII> q;
q.push({x, y});
while (q.size())
{
auto p = q.front();
q.pop();
for (int i = 0; i < 4; i++)
{
int a = p.x + dx[i], b = p.y + dy[i];
if (valid(a, b) && maze[a][b] != '#' && res[a][b] == -1)
{
res[a][b] = res[p.x][p.y] + 1;
q.push({a, b});
}
}
}
return res;
}
int minimalSteps(vector<string>& maze) {
n = maze.size(), m = maze[0].size();
vector<PII> buttons, stones;
int sx, sy, tx, ty;
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
if (maze[i][j] == 'M') buttons.push_back({i, j});
else if (maze[i][j] == 'O') stones.push_back({i, j});
else if (maze[i][j] == 'S') sx = i, sy = j;
else if (maze[i][j] == 'T') tx = i, ty = j;
// 初始化
int nb = buttons.size(), ns = stones.size();
vector<vector<int>> start_d = bfs(sx, sy, maze);
// 没有机关
if (nb == 0) return start_d[tx][ty];
// 从某个机关到其他机关 / 起点与终点的最短距离
vector<vector<int>> d(nb, vector<int>(nb + 2, -1));
vector<vector<vector<int>>> tmp(nb);
for (int i = 0; i < nb; i++)
{
tmp[i] = bfs(buttons[i].x, buttons[i].y, maze);
// 从某个点到终点不需要拿石头
d[i][nb + 1] = tmp[i][tx][ty];
}
for (int i = 0; i < nb; i++)
{
int t = -1;
// 找 起点 - 石头 - 机关 的最短距离
for (int k = 0; k < ns; k++)
{
int mid_x = stones[k].x, mid_y = stones[k].y;
if (tmp[i][mid_x][mid_y] != -1 && start_d[mid_x][mid_y] != -1)
if (t == -1 || t > tmp[i][mid_x][mid_y] + start_d[mid_x][mid_y])
t = tmp[i][mid_x][mid_y] + start_d[mid_x][mid_y];
}
d[i][nb] = t;
// 找 机关 - 石头 - 机关 的最短距离
for (int j = i + 1; j < nb; j++)
{
int mn = -1;
for (int k = 0; k < ns; k++)
{
int mid_x = stones[k].x, mid_y = stones[k].y;
if (tmp[i][mid_x][mid_y] != -1 && tmp[j][mid_x][mid_y] != -1)
if (mn == -1 || mn > tmp[i][mid_x][mid_y] + tmp[j][mid_x][mid_y])
mn = tmp[i][mid_x][mid_y] + tmp[j][mid_x][mid_y];
}
d[i][j] = mn;
d[j][i] = mn;
}
}
// 无解情况
for (int i = 0; i < nb; i++)
if (d[i][nb] == -1 || d[i][nb + 1] == -1) return -1;
int f[1 << nb][nb];
memset(f, -1, sizeof f);
for (int i = 0; i < nb; i++)
f[1 << i][i] = d[i][nb];
// 由于更新的状态都比未更新的大,所以直接从小到大遍历即可
// 板
for (int msk = 1; msk < 1 << nb; msk++)
for (int i = 0; i < nb; i++)
if (msk >> i & 1)
for (int j = 0; j < nb; j++)
if ((msk >> j & 1) == 0)
if (f[msk | (1 << j)][j] == -1 || f[msk | (1 << j)][j] > f[msk][i] + d[i][j])
f[msk | (1 << j)][j] = f[msk][i] + d[i][j];
int res = -1;
for (int i = 0; i < nb; i++)
if (res == -1 || res > f[(1 << nb) - 1][i] + d[i][nb + 1])
res = f[(1 << nb) - 1][i] + d[i][nb + 1];
return res;
}
};前缀和优化 DP
https://atcoder.jp/contests/abc253/tasks/abc253_e 输入 n(2≤n≤1000) m k(0≤k<m≤5000)。 输出有多少个长为 n 的数组,满足元素范围为 [1,m] 且 abs(a[i]-a[i+1]) >= k。 模 998244353。
前缀和优化 DP。
定义 f[i][j] 表示考虑前 i 个数,其中 a[i]=j 的方案数。
根据要求,从所有 abs(j-j') >= k 的 f[i-1][j'] 转移过来,这个和式可以用前缀和优化成 O(1)。
初始值 f[1][j] = 1。
答案为 sum(f[n-1])。
代码细节较多,注意循环 i 从 2 开始,j 从 0 开始
本来应是加法,但由于是两头的前缀和,因此可优化成总的减去中间段
LL s[N], pre[N];
int n, m, k;
int main()
{
scanf("%d%d%d", &n, &m, &k);
for (int i = 1; i <= m; i++) pre[i] = i;
for (int i = 2; i <= n; i++)
{
for (int j = 0; j < m; j++)
{
LL f = pre[m];
if (k > 0) f -= pre[min(j + k, m)] - pre[max(j - k + 1, 0)];
s[j + 1] = (s[j] + f) % mod;
}
for (int i = 0; i <= m; i++) pre[i] = s[i];
}
printf("%lld\n", (s[m] + mod) % mod);
return 0;
}余数背包 DP
https://atcoder.jp/contests/abc262/tasks/abc262_d 输入 n(1≤n≤100) 和长为 n 的数组 a(1≤a[i]≤1e9)。 如果一个非空子序列的平均值是整数,那么称其为漂亮的。 输出 a 的漂亮子序列的个数,模 998244353。 注:子序列不一定连续。
枚举子序列的长度。
考虑子序列长度固定为 m 时,有多少个平均值为整数的子序列。
相当于子序列的元素和模 m 为 0。
用选或不选来思考。
定义 f[i][j][k] 表示从前 i 个数中选 j 个数,元素和模 m 为 k 的方案数。
为方便计算取模,用刷表法(用查表法的话,需要算 (k-a[i])%m,可能会算出负数):
f[i][j][(k+a[i])%m] = f[i-1][j][(k+a[i])%m] + f[i-1][j-1][k]
答案为 f[n][m][0]。
代码实现时,第一个维度可以去掉,然后像 0-1 背包那样倒序循环 j。初始值 f[0][0] = 1。
余数背包 DP ,复杂度是 O(n4) ?
int a[110], f[110][110][110];
int n;
int res;
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
for (int m = 1; m <= n; m++)
{
memset(f, 0, sizeof f);
f[0][0][0] = 1;
for (int i = 1; i <= n; i++)
for (int j = 0; j <= m; j++)
for (int k = 0; k < m; k++)
{
f[i][j][k] = (f[i][j][k] + f[i - 1][j][k]) % mod;
if (j) f[i][j][(k + a[i]) % m] = (f[i][j][(k + a[i]) % m] + f[i - 1][j - 1][k]) % mod;
}
res = (res + f[n][m][0]) % mod;
}
printf("%d\n", res);
return 0;
}期望 DP 入门
https://atcoder.jp/contests/abc280/tasks/abc280_e 输入 n(1≤n≤2e5) p(0≤p≤100) 怪物的血量为 n。 每次攻击,有 p/100 的概率会对怪物造成 2 点伤害,有 1-p/100 的概率会造成 1 点伤害。 让怪物血量 <= 0,攻击次数的期望是多少? 假设期望等于分数 a/b,你需要输出 a * pow(b, mod-2) % mod,其中 mod=998244353。
期望 DP 入门题。
用 f[i] 表示血量为 i 时的攻击次数的期望。
那么 f[i] = p/100 * (f[i-2]+1) + (1-p/100) * (f[i-1]+1)
初始值 f[0]=0, f[1]=1。
答案为 f[n]。
实现上考虑预处理出来逆元
int n, p;
LL f[N];
int qmi(int a, int k, int p) // 求a^k mod p
{
int res = 1 % p;
while (k)
{
if (k & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
int main()
{
scanf("%d%d", &n, &p);
f[1] = 1;
int inv = qmi(100, mod - 2, mod);
for (int i = 2; i <= n; i++)
f[i] = (f[i - 2] * p + f[i - 1] * (100 - p) + 100) % mod * inv % mod;
printf("%lld\n", f[n]);
return 0;
}分割数组求每段乘积和
https://atcoder.jp/contests/abc288/tasks/abc288_f 输入 n(2≤n≤2e5) 和长为 n 的数字 s,保证 s 不含 0。 把 s 分割成若干段,得分为每一段的乘积。特别地,如果不分割,则得分为 s。 输出所有分割方案的得分之和,模 998244353。 注:一共有 2^(n-1) 种分割方案。
提示 1:从划分型 DP 入手,你能否找到一个规模更小的子问题?
例如 s=1234,如果最后一段为 34,那么得分为 1234+1234 = (12+12)*34。
注意 12+1*2 是 12 的所有划分的得分之和。
由此可见,枚举出最后一段后,我们可以把问题变成一个规模更小的子问题。
提示 2:定义 f[i] 表示分割前 i 个数字的得分之和(i 从 1 开始)
f[0] = 0
f[i] = val(1,i) + f[1]*val(2,i) + f[2]*val(3,i) + ... + f[i-1]*val(i,i)
其中 val(j,i) 表示 s[j] 到 s[i] 这一段对应的数字。
但这样写是 O(n^2) 的。
提示 3:观察 f[i-1] 的转移方程与 f[i] 的转移方程的差异。
提示 4:val(j,i) = val(j,i-1) * 10 + (s[i] - '0')
根据这一式子可以得到
f[i] = f[i-1] * 10 + (1+f[1]+f[2]+...+f[i-1]) * (s[i] - '0')
所以再用一个变量 sumF 表示 1+f[1]+f[2]+...+f[i-1],就可以 O(1) 地从 f[i-1] 算出 f[i] 了。
LL f[N];
char a[N];
int main()
{
int n;
scanf("%d%s", &n, a + 1);
f[0] = 0;
LL s = 1;
for (int i = 1; i <= n; i++)
{
f[i] = (s * (a[i] - '0') % mod + 10 * f[i - 1] % mod) % mod;
s += f[i];
}
printf("%lld\n", f[n]);
return 0;
}模数分类 DP
https://codeforces.com/problemset/problem/1105/C 输入正整数 n(<=2e5),l 和 r(1<=l<=r<=1e9)。 求有多少个不同的长为 n 的数组,数组元素值的范围为 [l,r],且数组元素之和为 3 的倍数。 答案对 1e9+7 取模。
按模数分类的 DP
定义 f[i][0/1/2] 表示长为 i,元素和为 0/1/2 的数组个数。
枚举第 i 个数所填的数字模 3 的结果,那么 f[i][0] = f[i-1][0]*c[0] + f[i-1][1]*c[2] + f[i-1][2]*c[1],其余同理。
其中 c[0/1/2] 为 [l,r] 内模 3 余 0/1/2 的数字个数,计算这个可以考虑用 [0,r] 范围内的减去 [0,l-1] 范围内的。计算这个的方法看代码(怎么理解好呢)
cin >> n >> l >> r;
int c[3] = {};
l --;
c[0] = r / 3 - l / 3; //r / 3 - (l + 2) / 3 + 1;
c[1] = (r + 2) / 3 - (l + 2) / 3; //(r - 1) / 3 - (l - 1 + 2) / 3 + 1;
c[2] = (r + 1) / 3 - (l + 1) / 3; //(r - 2) / 3 - (l - 2 + 2) / 3 + 1;
LL f[3] = {1}, g[3] = {};
for (int i = 0; i < n; i++)
{
g[0] = (f[0] * c[0] + f[1] * c[2] + f[2] * c[1]) % MOD;
g[1] = (f[0] * c[1] + f[1] * c[0] + f[2] * c[2]) % MOD;
g[2] = (f[0] * c[2] + f[1] * c[1] + f[2] * c[0]) % MOD;
for (int j = 0; j < 3; j++) f[j] = g[j];
}
cout << f[0] << endl;新奇 DP 一次考虑连续三个点
https://codeforces.com/contest/358/problem/D 给你 3 个长度均为 n(<=3000) 的数组 a b c,元素范围 [0,1e5],具体含义见下文。 有 n 个物品排成一排,你可以按照任意顺序拿物品,并获得相应的分数:
- 如果拿走某个物品时,相邻两个物品都没有被拿过,那么得到的分数为 a[i]
- 如果相邻的两个物品恰好有一个被拿过,那么得到的分数为 b[i]
- 如果相邻的两个物品都被拿走了,那么得到的分数为 c[i] 问拿走所有物品后,能够获得的最高分数为多少?
很新奇的 DP 题。难点在于,每个点的决策会影响前后两个点,前后两个点的决策也会影响到当前点
怎么思考?考虑到第 i 个数时,把 i-2, i-1, i 这三个点合在一起思考,想想看这三个点的先后顺序怎么影响第 i-1 个数对答案的贡献
定义 f[i][1] 表示先拿 i-1,再拿 i 的方案集合,属性是前 i-1 个数的最大分数
同理 f[i][0] 表示先拿 i,再拿 i-1 的方案集合
要先拿 i-1,再拿 i,考虑一下 i-1 和 i-2 的先后顺序
- 如果先拿 i-2,那么拿 i-1 时,贡献就取 b[i-1]
- 否则,拿 i-1 时左右都还没被拿走,贡献取 a[i-1]
对另一种情况的分析同理
边界怎么考虑?
- 由于是取 max,因此所有状态初始化为负无穷
- 对于第一个数,只能是先取这个点,即 f[1][0] = 0
- 对于最后一个数,只能是先取这个点,故 f[n+1][1] 就是答案
memset(f, -0x3f, sizeof f);
f[1][0] = 0;
for (int i = 2; i <= n + 1; i++)
{
f[i][1] = max(f[i - 1][1] + b[i - 1], f[i - 1][0] + a[i - 1]);
f[i][0] = max(f[i - 1][1] + c[i - 1], f[i - 1][0] + b[i - 1]);
}
cout << f[n + 1][1] << endl;简单子序列 DP
https://codeforces.com/problemset/problem/209/A 求一个长为 n(<=1e6) 的 01 交替串中有多少个 01 交替子序列。对结果模 1e9+7。 注意子序列不要求连续。
典中典 DP,代码说话
int endsWith1 = 0, endsWith0 = 0, nothing = 1;
for (int i = 0; i < n; i++)
if (i % 2) endsWith1 = (0LL + endsWith1 + endsWith0 + nothing) % MOD;
else endsWith0 = (0LL + endsWith1 + endsWith0 + nothing) % MOD;
cout << (0LL + endsWith0 + endsWith1) % MOD << endl;子序列不含 hard 的方案数
https://codeforces.com/problemset/problem/1096/D 给你一个 n(<=1e5),一个长为 n 的字符串 s 和一个长为 n 的数组 a(1<=a[i]<=998244353)。 表示每个 s[i] 都有一个对应的删除代价 a[i]。 请你删除 s 中的某些字符,使得 s 不包含 "hard" 子序列。 输出被删除字母的代价之和的最小值。 子序列不要求连续。s 仅包含小写字母。
DP 典题
看到子序列就要往 DP 上想。
先来讨论不包含 hard 子序列需要怎么删。
对于第 i 个字符:
不删:那么前 i-1 个字符不能包含 har 子序列(否则就构成 hard 子序列了)。
删:那么前 i-1 个字符可以包含 har 子序列,但不能包含 hard 子序列。
这样思考一番后,定义 dp[i][j=1/2/3/4] 表示删除 s 的前 i 个字符中的某些字符,使得结果不包含 "hard"[:j] 子序列的最小代价("hard"[:j] 表示 "hard" 的长为 j 的前缀)。
如果 s[i] 是 "hard" 的第 j 个字符,那么有
dp[i][j] = min(dp[i-1][j-1], dp[i-1][j]+a[i])
表示不删 or 删,取二者最小值。
注意对于 dp[i][1] 来说,在遇到 "h" 时必须删除,因此可以把 dp[i][0] 初始化成 inf 从而简化逻辑。
如果 s[i] 不在 "hard" 中,转移就是 dp[i] = dp[i-1]
答案为 dp[n][4]。
实现时可以用滚动数组优化掉第一维。
dp[i][1/2/3/4] 分别表示
不能有 h
不能有 ha(可以有 h)
不能有 har(可以有 ha)
不能有 hard(可以有 har)
LL f[4] = {0};
for (char c: s)
{
cin >> v;
switch (c) {
case 'h': f[0] += v; break;
case 'a': f[1] = min(f[0], f[1] + v); break;
case 'r': f[2] = min(f[1], f[2] + v); break;
case 'd': f[3] = min(f[2], f[3] + v); break;
}
}
cout << f[3] << endl;全新形式的 DP
https://codeforces.com/problemset/problem/933/A 输入 n (≤2000) 和一个长为 n 的数组 a,元素值只有 1 和 2。 你可以翻转 a 的一个区间(该操作执行至多一次)。 输出你能得到的最长非降子序列的长度。 子序列不要求连续。
答案的组成一定是 [1,1,...][2,2,...][1,1,...][2,2,...] 这样四段子序列(每一段都允许为空),然后翻转二三段的到答案,那么用 f[i][0/1/2/3] 维护前 i 个数中前 j 段的最大长度即可
for (int i = 0; i < n; i++)
{
cin >> x;
f[0] += x == 1;
f[1] = max(f[0], f[1] + (x == 2));
f[2] = max(f[1], f[2] + (x == 1));
f[3] = max(f[2], f[3] + (x == 2));
}
cout << f[3] << endl;理解了很久的单调栈 DP
https://codeforces.com/problemset/problem/1407/D 输入 n(≤3e5) 和一个长为 n 的数组 h (1≤h[i]≤1e9)。 满足如下三个条件之一,就可以从 i 跳到 j (i<j):
- i+1=j
- max(h[i+1],...,h[j-1]) < min(h[i],h[j])
- min(h[i+1],...,h[j-1]) > max(h[i],h[j]) 输出从 1 跳到 n 最少需要多少步。
以条件二为例,自己做的时候先画个图分析一下,会发现 i 往左扫到第一个大于等于 h[j] 的位置时,i 的左边就不可能作为转移来源了,那么首先要找到左边第一个不大于 h[j] 的位置,这启发我们用单调栈解决。继续观察发现,如果用严格单调递减的栈来维护,那么在 i 和 j 之间,且可以作为转移来源的位置,恰好就在栈中,而且会在寻找 i 的时候顺便出栈,那么就可以边出栈边更新 f[j] 了
下面难以理解的地方在于代码中,为什么先 pop 一次,还要比较是否相等才更新呢?我的理解是,在循环到 i-1 时,栈中已经构建出了以 a[i-1] 为最小值的单调递减格局,在循环到 i 时,i-1 肯定在栈中,但是不需要理会,因为 i-1 在条件一时就处理了,相当于从单调栈的倒数第二个位置开始比对。还有一个点,虽然是在寻找“大于等于”的位置,但是结合题意得知,当遇到了 a[i]==a[j] 时,i 左侧的位置是不能作为转移来源的,因此要设置一个 flag 位,遇到 a[s.top()] == a[j] 时置 1,之后正常弹栈但是不更新 f[j]。把以上两点综合起来,并且免去设置 flag 的写法,就是下面的代码,仔细体会(每次 pop 一个数,实际上在关心栈中的下一个数)
memset(f, 0x3f, sizeof f);
f[0] = -1;
for (int i = 1; i <= n; i++)
{
f[i] = f[i - 1] + 1;
while (desc.size() && a[i] >= a[desc.top()])
{
int x = desc.top();
desc.pop();
if (desc.size() && a[x] != a[i]) f[i] = min(f[i], f[desc.top()] + 1);
}
/*
等价写法
bool flag = 1;
while (desc.size() && a[i] >= a[desc.top()])
{
int x = desc.top();
desc.pop();
f[i] = min(f[i], f[x] + 1);
if (a[x] == a[i]) flag = 0;
}
if (flag && desc.size()) f[i] = min(f[i], f[desc.top()] + 1);
*/
while (asc.size() && a[i] <= a[asc.top()])
{
int x = asc.top();
asc.pop();
if (asc.size() && a[x] != a[i]) f[i] = min(f[i], f[asc.top()] + 1);
}
desc.push(i), asc.push(i);
}
cout << f[n] << endl;二分答案,用树形 DP 来 check
http://codeforces.com/problemset/problem/1739/D 输入 t(≤1e4) 表示 t 组数据,每组数据输入 n k(0≤k<n≤2e5),有一颗 n 个节点的树,输入 n-1 个数 p[2],p[3],...,p[n],p[i] 表示点 i 的父节点为 p[i]。 所有数据的 n 之和不超过 2e5。 你可以做如下操作至多 k 次: 断开 p[i] 和 i 之间的边,然后在 1 和 i 之间连边。 输出操作后,这颗树的最小高度。 高度的定义为 1 到最远叶子节点的路径的边数。
提示 1:由于最终的树越高,操作次数越少,最终的树越矮,操作次数越多,满足单调性,因此可以二分答案。
提示 2:check 需要写一个树形 DP,自底向上计算最长路径长度,达到 mid-1 的时候,切断当前节点和父节点的边,计数器 cnt++,如果最后 cnt≤k 则说明答案不超过 mid。
写 check 的时候逻辑错了很多次,需要梳理清楚当前考虑的深度要不要 +1
int dfs(int u, int fa)
{
int d = 0;
// 错误写法一
// for (int v: g[u])
// if (v != fa)
// d = max(d, dfs(v, u) + 1);
// if (d == m - 1 && fa != 1) cnt ++, d = 0;
// return d;
// 错误写法二
// for (int v: g[u])
// if (v != fa)
// {
// int t = dfs(v, u);
// if (t == m - 1 && u != 1) cnt ++, t = 0;
// d = max(d, t + 1);
// }
// return d;
for (int v: g[u])
if (v != fa)
{
int t = dfs(v, u);
if (t == m - 1 && u != 1) cnt ++;
else d = max(d, t + 1);
}
return d;
}树中上下走的换根 DP
https://atcoder.jp/contests/abc222/tasks/abc222_f 输入 n(2≤n≤2e5) 和一棵树的 n-1 条边(节点编号从 1 开始),每条边输入两个端点和边权。 然后输入 n 个数 d,d[i] 表示点 i 的点权。 定义 f(x,y) = 从 x 到 y 的简单路径的边权之和,再加上 d[y]。 定义 g(x) = max{f(x,i)},这里 i 取遍 1~n 的所有不为 x 的点。 输出 g(1),g(2),...,g(n)。
思路是从 1 开始 dfs,记录从每棵子树的根往下走能得到的最大值 fi 和次大值 se,以及哪个子树可以得到最大值。
然后换根,从 v 到 w,把根从 v 换成 w:如果 w 是 v 的最大值对应的子树,那么对于 w 来说,它往上走能得到的最大值可以是 v 的 se,否则往上走能得到的最大值可以是 v 的 fi。
由于 g(x,y) 和 d[y] 有关,所以对于 w 来说,往上走的最大值还需要与 d[v]+(v->w 的边权) 求最大值。具体见代码。
struct {
LL fi, se;
int i;
} ans[N];
LL res[N];
void dfs(int u, int fa)
{
for (auto &[v, w]: g[u])
if (v != fa)
{
dfs(v, u);
LL r = max(ans[v].fi, (LL)d[v]) + w;
if (r > ans[u].fi) ans[u] = {r, ans[u].fi, v};
else if (r > ans[u].se) ans[u].se = r;
}
}
void dp(int u, int fa, LL up)
{
res[u] = max(ans[u].fi, up);
up = max(up, (LL)d[u]);
for (auto &[v, w]: g[u])
if (v != fa)
{
LL down = ans[u].fi;
if (v == ans[u].i) down = ans[u].se;
dp(v, u, max(up, down) + w);
}
}由 1 和-1 构成的矩阵,问是否存在和为 0 的路径
https://codeforces.com/problemset/problem/1695/C 输入 t(≤1e4) 表示 t 组数据,每组数据输入 n(≤1e3) m(≤1e3) 和一个 n 行 m 列的矩阵,元素值只有 -1 和 1。所有数据的 n*m 之和不超过 1e6。 你从矩阵左上出发,走到右下,每步只能向下或者向右。 路径上的元素和能否为 0?输出 YES 或 NO。
提示 1:交换路径中的相邻两步,比如向右向下变成向下向右,路径和会发生什么变化?
路径和会 +0/+2/-2。
因此,如果 n+m 是偶数,路径和必然为奇数,无法变成 0。此时可以直接输出 NO。
如果 n+m 是奇数,路径和必然为偶数,然后要怎么判断?
提示 2:求出最小路径和以及最大路径和,如果一个 <=0,一个 >=0,根据提示 1,可以通过交换,变成 0。(不必思考具体怎么走,而是转化为一个取值范围问题,具体方案的证明看 tutorial)
怎么求?这是个经典 DP,见 LC64
mn[0][0] = mx[0][0] = g[0][0];
for (int i = 1; i < n; i++)
mx[i][0] = mn[i][0] = mx[i - 1][0] + g[i][0];
for (int i = 1; i < m; i++)
mx[0][i] = mn[0][i] = mx[0][i - 1] + g[0][i];
for (int i = 1; i < n; i++)
for (int j = 1; j < m; j++)
{
mx[i][j] = max(mx[i - 1][j], mx[i][j - 1]) + g[i][j];
mn[i][j] = min(mn[i - 1][j], mn[i][j - 1]) + g[i][j];
}
if ((m + n) % 2 == 0 || mn[n - 1][m - 1] > 0 || mx[n - 1][m - 1] < 0) cout << "NO" << endl;
else cout << "YES" << endl;树中与距离最远的点有关的换根 DP
codeforces.com/problemset/problem/337/D 输入 n m(1≤m≤n≤1e5) d(0≤d≤n-1) 表示一棵 n 个节点的树,其中 m 个节点有怪物,这些怪物是由一个传送门生成的,传送门与任意怪物的距离不超过 d。 然后输入 m 个互不相同的数,表示怪物所在节点编号(从 1 开始)。 然后输入 n-1 行,每行两个节点编号,表示树的边。 输出可能存在传送门的节点的个数。注意传送门只有一个。
第一思路:以 r 为根时,距离最远的怪物点要么在 r 为根的子树中,要么在子树外,因此需要知道 distDown[] 和 distUp[],如果 max <= d,那么 r 是可以作为传送门节点的
第一次 DFS 以 1 为根,对每个点记录往下走的最远怪物距离和次远怪物距离,以及最远怪物在哪棵子树中。
第二次 DFS,从 v 到 w 时:
如果 w 是 v 的最远怪物所在子树,那么 w 往上的最远怪物距离就是 max(v 往上最远怪物距离, v 往下次远怪物距离)+1;
如果 w 不是 v 的最远怪物所在子树,那么 w 往上的最远怪物距离就是 max(v 往上最远怪物距离, v 往下最远怪物距离)+1。
对于一个点 v,如果 v 往上往下的最远怪物距离都不超过 d,那么 v 就可能是传送门所在位置。
struct {
int fi, se, fv;
} ans[N];
int dfs(int u, int fa)
{
ans[u].fi = ans[u].se = -1e9;
for (int v: g[u])
if (v != fa)
{
int dis = dfs(v, u) + 1;
if (dis > ans[u].fi)
ans[u].se = ans[u].fi, ans[u].fi = dis, ans[u].fv = v;
else if (dis > ans[u].se) ans[u].se = dis;
}
if (ans[u].fi < 0 && st[u]) return 0;
return ans[u].fi;
}
void dp(int u, int fa, int dFa) // dp(1, 0, -1e9)
{
if (dFa > d) return;
if (ans[u].fi <= d) res ++; // up <= d && down <= d
if (st[u] && dFa < 0) dFa = 0;
for (int v: g[u])
if (v != fa)
{
if (v == ans[u].fv) dp(v, u, max(dFa, ans[u].se) + 1);
else dp(v, u, max(dFa, ans[u].fi) + 1);
}
}字符串划分方案 DP
https://codeforces.com/problemset/problem/1624/E 输入 t(≤1e4) 表示 t 组数据。所有数据的 n*m 之和 ≤1e6。 每组数据输入 n(≤1e3) m(≤1e3) 和长为 n 的字符串数组 a。 然后再输入一个字符串 s。 所有字符串长度均为 m,仅包含 '0'~'9'。 你需要将 s 划分成若干个长度至少为 2 的子串,且每个子串都是某个 a[i] 的子串(不同子串对应的 a[i] 可以不同)。 如果无法划分,输出 -1;否则输出划分出的子串个数 k,然后输出 k 行,每行三个数字 l r i,表示这个子串等于 a[i] 的子串 [l,r]。注意 l r i 的下标均从 1 开始。注意输出的 k 行要与划分的顺序相同。 如果有多种划分方案,输出任意一种。
本题知识点:任意 >=4 的数字都可以拆分为若干 2 和 3 的和。
提示 1:预处理所有长为 2 和 3 的子串及其位置。
提示 2:线性 DP,定义 f[i] 表示能否拆分 s[:i],那么 f[i] 从 f[i-2] 或 f[i-3] 转移,需要看末尾能拆出 2 个字符还是 3 个字符。
f[0]=true,答案为 f[n]。
for (int i = 1; i <= n; i++)
{
cin >> s;
for (int r = 2; r <= m; r++)
{
mp[s.substr(r - 2, 2)] = {r - 1, r, i};
if (r > 2) mp[s.substr(r - 3, 3)] = {r - 2, r, i};
}
}
cin >> s;
vector<bool> f(m + 1);
f[0] = 1;
for (int i = 2; i <= m; i++)
f[i] = (f[i - 2] && mp[s.substr(i - 2, 2)].l > 0) ||
(i > 2 && f[i - 3] && mp[s.substr(i - 3, 3)].l > 0);
vector<tup> res;
for (int i = m; i; )
if (f[i - 2] && mp[s.substr(i - 2, 2)].l > 0)
{
res.push_back(mp[s.substr(i - 2, 2)]);
i -= 2;
}
else
{
res.push_back(mp[s.substr(i - 3, 3)]);
i -= 3;
}用记忆化搜索实现区间 DP
https://codeforces.com/problemset/problem/149/D 输入一个合法括号字符串,仅包含 '(' 和 ')',长度范围 [2,700]。 对括号染色,必须满足如下所有条件:
- 一个括号可以染成红色、蓝色或者不染色。
- 对于一对匹配的括号,恰好其中一个被染色。
- 两个相邻的染了色的括号,颜色不能相同。 求染色方案数,模 1e9+7。
首先预处理每个左括号对应的右括号的位置,用栈来处理。
由于是从外到内递归,从内到外转移,所以是区间 DP
DP 除了记录区间左右端点 l r 外,为了判断条件 3,还需要记录 l-1 和 r+1 的颜色。
然后就是分类讨论了
// int f[n][n][3][3];
memset(f, -1, sizeof f);
function<int(int, int, int, int)> dfs = [&](int l, int r, int lc, int rc)
{
if (l > r) return 1;
int &p = f[l][r][lc][rc];
if (p != -1) return p;
int mid = right[l];
LL res = 0;
if (mid < r)
{
res += 1LL * dfs(l + 1, mid - 1, 0, 1) * dfs(mid + 1, r, 1, rc);
res += 1LL * dfs(l + 1, mid - 1, 0, 2) * dfs(mid + 1, r, 2, rc);
if (lc != 1) res += 1LL * dfs(l + 1, mid - 1, 1, 0) * dfs(mid + 1, r, 0, rc);
if (lc != 2) res += 1LL * dfs(l + 1, mid - 1, 2, 0) * dfs(mid + 1, r, 0, rc);
}
else
{
if (lc != 1) res += dfs(l + 1, r - 1, 1, 0);
if (lc != 2) res += dfs(l + 1, r - 1, 2, 0);
if (rc != 1) res += dfs(l + 1, r - 1, 0, 1);
if (rc != 2) res += dfs(l + 1, r - 1, 0, 2);
}
p = res % MOD;
return p;
};
cout << dfs(0, n - 1, 0, 0) << endl;前缀和优化 DP(数轴上移动的方案数)
https://codeforces.com/contest/480/problem/C 输入整数 n a b k (2≤n≤5000, 1≤k≤5000, 1≤a,b≤n, a≠b)。 你需要从数轴上的 a 出发,移动恰好 k 次。 从整数 x 移动到整数 y,必须满足以下所有要求:
- 1≤y≤n
- y≠x
- y≠b
- |x-y|<|x-b| 输出不同移动方案的个数,模 1e9+7。
难点在于第四个条件,会发现是不能移动到 b 及其右边的
前缀和优化 DP。
为方便计算,如果 a>b,根据对称性调整为 a=n+1-a,b=n+1-b。这样可以保证 a<b。
定义 f[i][j] 表示 i 次移动后,移动到 j 的方案数。f[0][a] = 1。1≤j<b。
考虑从位置 x 转移过来:
如果 x<j,可以移动到 j。
如果 x>j,根据要求 4,解不等式得 x≤j+floor((b-y-1)/2)。
所以 f[i][j] = f[i-1][1] + ... + f[i-1][j+floor((b-y-1)/2)] - f[i-1][j]。
最后的减法是因为要求 2。
答案为 sum(f[k][j])。
if (a > b) a = n + 1 - a, b = n + 1 - b;
vector<LL> f(b), s(n + 1);
f[a] = 1;
while (k -- )
{
for (int i = 0; i < b; i++) s[i + 1] = s[i] + f[i];
for (int y = 1; y < b; y++)
f[y] = (s[y + (b - y - 1) / 2 + 1] - f[y]) % MOD;
}
LL res = 0;
for (int i = 0; i < b; i++) res += f[i];
cout << res % MOD << endl;子序列和转换为背包问题
https://codeforces.com/contest/1516/problem/C 输入 n(2≤n≤100) 和长为 n 的数组 a(1≤a[i]≤2000)。 你需要删除 a 中的一些数,使 a 无法分成两个元素和相等的子序列。 输出最少要删除多少个数,以及这些数的下标(从 1 开始)。 注:子序列不要求连续。
分类讨论:
- 如果 sum(a) 是奇数,显然没法分,无需删除任何数字,输出 0。
- 如果无法从 a 中选出元素和等于 sum(a)/2 的子序列,那么也没法分,输出 0。这可以用 0-1 背包判断。
- 否则就可以分,那么要如何删除呢?此时 sum(a) 是偶数,由于偶数 - 奇数 = 奇数,所以减去一个奇数即可。
- 要是没有奇数呢?此时每个 a[i] 都是偶数,那么把每个 a[i] 都除以 2,是不会影响答案的。反复除以 2 直到 a 中有奇数为止。
代码实现时,无需反复除以 2,而是除以最小的 lowbit(a[i])。如果要删除数字,也是删除 lowbit 最小的数。
for (int i = 0; i < n; i++)
{
cin >> a[i];
tot += a[i];
int lb = lowbit(a[i]);
if (lb < mn)
{
mn = lb;
idx = i;
}
}
tot /= mn;
if (tot % 2) cout << 0 << endl;
else
{
f[0] = 1;
for (int i = 0; i < n; i++)
{
a[i] /= mn;
for (int j = tot; j >= a[i]; j--)
f[j] |= f[j - a[i]];
}
f[tot / 2] ? (cout << 1 << endl << idx + 1 << endl) : (cout << 0 << endl);
}位运算结合划分型 DP
https://codeforces.com/problemset/problem/981/D 输入 n k(1≤k≤n≤50) 和长为 n 的数组 a(0<a[i]<2^50)。 把 a 划分成恰好 k 个非空连续子数组。 把第 i 个子数组记作 b[i]。 最大化 sum(b[0]) AND sum(b[1]) AND ... AND sum(b[k-1])。 这里 AND 表示按位与。
涉及到二进制的题目,其中一种思路是拆位。
设最高位为 m。
第 m 位能不能是 1?如果能,那么答案至少是 1<<m。
怎么判断?标准的划分型 DP,定义 f[i][r] 表示 a[0] 到 a[r-1] 能否分成 i 段,且每一段的第 m 位都是 1。
设 target = 1<<m,有
f[i][r] |= f[i-1][l] && ((sum[r] - sum[l]) & target) == target
其中 sum[0] = 0, sum[i] = a[0] + ... + a[i-1]
初始值 f[0][0] = true,如果最后 f[k][n] = true 则说明第 m 位可以是 1。
然后继续判断,第 m-1 位能不能是 1?第 m-2 位能不能是 1?……
注意如果第 m 位是 1,那么在判断其余位的时候,要带着第 m 位是 1 一块判断。(代码中压缩成一维,所以每轮循环后 f[0] = 0)
for (int i = 64 - __builtin_clzll(sum[n]); i >= 0; i--)
{
LL bit = 1LL << i;
LL target = res | bit;
vector<bool> f(n + 1);
f[0] = 1;
for (int i = 0; i < k; i++)
{
for (int r = n; r; r--)
{
f[r] = 0;
for (int l = 0; l < r; l++)
if (f[l] && ((sum[r] - sum[l]) & target) == target)
{
f[r] = 1;
break;
}
}
f[0] = 0;
}
if (f[n]) res = target;
}前后缀积解决逆元 + 换根 DP
https://codeforces.com/problemset/problem/543/D 输入 n(2≤n≤2e5) 和 n-1 个数 p2,p3,...,pn,表示一棵 n 个节点的无根树,节点编号从 1 开始,i 与 pi(1≤pi≤i-1) 相连。 定义 a(x) 表示以 x 为根时的合法标记方案数,模 1e9+7。其中【合法标记】定义为:对树的某些边做标记,使得 x 到任意点的简单路径上,至多有一条边是被标记的。 输出 a(1),a(2),...,a(n)。
先来计算 a(1),此时 1 为树根。
定义 f(i) 表示子树 i 的合法标记方案数。
对于 i 的儿子 j,考虑 i-j 这条边是否标记:
- 标记:那么子树 j 的所有边都不能标记,方案数为 1。
- 不标记:那么方案数就是 f(j)。
i 的每个儿子互相独立,所以根据乘法原理有
f(i) = (f(j1)+1) * (f(j2)+1) * ... * (f(jm)+1)
其中 j1,j2,...,jm 是 i 的儿子。
然后来计算其余 a(i)。
考虑把根从 i 换到 j:
对于 j 来说,方案数需要在 f(j) 的基础上,再乘上【父亲 i】这棵子树的方案数,即 a(i) / (f(j)+1)。
所以 a(j) = f(j) * (a(i)/(f(j)+1) + 1)
本题的一个易错点是,f(j)+1 可能等于 M=1e9+7,取模会变成 0,但是 0 没有逆元。用前后缀积来解决,即不乘 f(j)+1
vector<LL> pre[N], suf[N]; // 前缀积 后缀积
void dfs(int u, int fa)
{
f[u] = 1;
for (int v: g[u])
if (v != fa)
{
dfs(v, u);
f[u] = f[u] * (f[v] + 1) % MOD;
}
}
void dp(int u, int fa)
{
res[u] = 1;
for (int v: g[u])
{
res[u] = res[u] * (f[v] + 1) % MOD;
if (v != fa)
pre[u].push_back(f[v] + 1), suf[u].push_back(f[v] + 1);
}
for (int i = 1; i < pre[u].size(); i++)
pre[u][i] = pre[u][i] * pre[u][i - 1] % MOD;
for (int i = suf[u].size() - 2; i >= 0; i--)
suf[u][i] = suf[u][i] * suf[u][i + 1] % MOD;
int cnt = 0; // 对应上面 push_back 的顺序
for (int v: g[u])
{
if (v == fa) continue;
f[u] = (fa ? f[fa] + 1 : 1);
if (cnt > 0) f[u] = f[u] * pre[u][cnt - 1] % MOD;
if (cnt < suf[u].size() - 1) f[u] = f[u] * suf[u][cnt + 1] % MOD;
dp(v, u);
cnt ++;
}
}字符串操作求方案数(区间 DP)
https://codeforces.com/problemset/problem/1336/C 输入长度不超过 3000 的字符串 S,只包含小写字母。设 S 的长度为 n。 输入长度不超过 n 的字符串 T,只包含小写字母。 从一个空字符串 A 开始,执行如下操作不超过 n 次: 删除 S 的第一个字母,然后加到 A 的开头或者末尾。 问:要使 T 是 A 的前缀,有多少种不同的操作方式?模 998244353。
先假设 s 和 t 一样长。
我们不知道 s 的第一个字母和谁匹配,但我们知道 s 的最后一个字母只能与 t[0] 或者 t[m-1] 匹配(加到开头或者末尾)。
假如与 t[0] 匹配,那么问题变成 s[:n-1] 与 t[1:] 匹配的方案数。这是一个规模更小的子问题。
这启发我们得到下面的区间 DP。
把 t 扩充成和 s 一样长,扩充的字母视作任意字符(一定可以与 s[i] 匹配)。
定义 f[i][j] 表示操作前缀 s[0]~s[j-i] 得到子串 t[i]~t[j] 的方案数。
那么答案就是 f[0][m-1]+f[0][m]+...+f[0][n-1]。
考虑 s[j-i] 与 t[i] 还是 t[j] 匹配,可以得到
f[i][j] = (i>=m || s[j-i]==t[i] ? f[i+1][j] : 0) + (j>=m || s[j-i]==t[j] ? f[i][j-1] : 0)
初始值 f[i][i] = (i>=m || s[0]==t[i] ? 2 : 0)
for (int i = 0; i < n; i++)
f[i][i] = (i >= m || s[0] == t[i]) ? 2 : 0;
for (int len = 2; len <= n; len++)
for (int i = 0; i + len - 1 < n; i++)
{
int j = i + len - 1;
if (i >= m || s[j - i] == t[i])
f[i][j] = (f[i][j] + f[i + 1][j]) % mod;
if (j >= m || s[j - i] == t[j])
f[i][j] = (f[i][j] + f[i][j - 1]) % mod;
}
LL res = 0;
for (int i = m - 1; i < n; i++)
res = (res + f[0][i]) % mod;逆向思维 转化为背包问题
https://codeforces.com/problemset/problem/730/J 输入 n(1≤n≤100) 和两个长为 n 的数组 a b (1≤a[i]≤b[i]≤100)。 有 n 个水桶,第 i 个水桶装了 a[i] 单位的水,水桶容量为 b[i]。 花费 1 秒,可以从某个水桶中,转移 1 个单位的水,到另一个水桶。 输出两个数: 把水汇集起来,最少需要多少个桶(换句话说需要倒空尽量多的桶),该情况下至少要多少秒完成?
最少需要多少个桶?这可以贪心地按照 b[i] 从大到小选择,直到选择的 b[i] 之和 >= sum(a) 为止。
假设最少需要 m 个桶。
在 m 个桶的前提下,至少要多少秒完成?
正难则反,考虑最多有多少单位的水是不需要转移的。
把 b[i] 看成物品体积,a[i] 看成物品价值,变成 0-1 背包问题:
定义 f[i][j][k] 表示从前 i 个桶中恰好选 j 个桶,这 j 个桶的容量之和恰好为 k 的情况下,最多有 f[i][j][k] 单位的水是不需要转移的。
状态转移方程为:f[i][j][k] = max(f[i-1][j][k], f[i-1][j-1][k-b[i]]+a[i])。
初始值:f[0][0][0] = 0,其余为负无穷大。
答案为:sum(a)-max(f[n][m][sum(a):])。
(注意这里我是用【恰好】定义的,k 需要从 sum(a) 枚举到 sum(b)。用【至少】定义 k 也是可以的。)
int f[m + 1][sb + 1];
memset(f, -0x3f, sizeof f);
f[0][0] = 0;
for (int i = 0; i < n; i++)
for (int j = m; j; j--)
for (int k = sb; k >= p[i].y; k--)
f[j][k] = max(f[j][k], f[j - 1][k - p[i].y] + p[i].x);
int mx = 0;
for (int i = sa; i <= sb; i++)
mx = max(mx, f[m][i]);
cout << m << ' ' << sa - mx << endl;字符串 方案数 转化为背包
https://www.luogu.com.cn/problem/P2679 输入 n(1≤n≤1000) m k(1≤k≤m≤200) 和长为 n 的字符串 s,长为 m 的字符串 t,只包含小写英文字母。 你需要从 s 中取出 k 个互不重叠的非空连续子串,然后把这 k 个子串按照其在 s 中的出现顺序依次连接起来,得到一个新的字符串。 输出有多少种方案可以使得这个新串与 t 相等。 答案模 1e9+7。 注意:子串相同但取出的位置不同,也认为是不同的方案。
朴素想法是枚举 f[i][j][k],然后看最后一段的长度,复杂度太高
优化:引入新维度,0/1 表示第 i 个字符包不包含在最后一个子串中
此外,本题还卡空间,观察转移方程,发现 f[i] 只与 f[i-1] 有关,于是优化掉一维
cin >> n >> m >> K >> a >> b;
// 看 a[i]: 0 表示不含,1 表示包含
// a[i] = b[j]: f[i][j][k][0] = f[i - 1][j][k][0] + f[i - 1][j][k][1] 即前面选或不选
// f[i][j][k][1] = f[i - 1][j - 1][k][1] + f[i - 1][j - 1][k - 1][0] + f[i - 1][j - 1][k - 1][1]
// a[i] != b[j]: f[i][j][k][0] = f[i - 1][j][k][0] + f[i - 1][j][k][1]
// f[i][j][k][1] = 0 由于选不了
f[0][0][0][0] = f[1][0][0][0] = 1;
bool t = 0;
for (int i = 1; i <= n; i++, t ^= 1)
for (int j = 1; j <= m; j++)
for (int k = 1; k <= K; k++)
{
f[t][j][k][0] = ((LL)f[t ^ 1][j][k][0] + f[t ^ 1][j][k][1]) % MOD;
if (a[i - 1] == b[j - 1])
f[t][j][k][1] = ((LL)f[t ^ 1][j - 1][k][1] + f[t ^ 1][j - 1][k - 1][0] + f[t ^ 1][j - 1][k - 1][1]) % MOD;
else f[t][j][k][1] = 0;
}
cout << ((LL)f[t ^ 1][m][K][0] + f[t ^ 1][m][K][1]) % MOD << endl;至少型 01 背包
https://atcoder.jp/contests/tenka1-2019/tasks/tenka1_2019_d 输入 n(3≤n≤300) 和长为 n 的数组 a(1≤a[i]≤300)。 把每个 a[i] 都涂成红/绿/蓝三种颜色中的一种。(相当于把 a 分成 3 个子序列) 记红色元素和为 R,绿色元素和为 G,蓝色元素和为 B。 问:有多少种涂色方案,使得 R,G,B 组成了一个非退化三角形的三条边。模 998244353。
正难则反 + 至少型 0-1 背包
int main()
{
scanf("%d", &n);
f[0] = g[0] = 3;
int pow3 = 1;
while (n -- )
{
scanf("%d", &v);
s += v;
for (int j = s; j >= 0; j--)
{
f[j] = (2LL * f[j] + f[max(j - v, 0)]) % mod; // 至少装满
if (j >= v) g[j] = ((LL)g[j] + g[j - v]) % mod; // 恰好装满
}
pow3 = 3LL * pow3 % mod;
}
if (s % 2 == 0) dup = g[s / 2]; // 恰好装满 s/2
int res = (LL)pow3 - (f[(s + 1) / 2] - dup);
printf("%d\n", (res % mod + mod) % mod);
return 0;
}排列型状压
https://codeforces.com/problemset/problem/1238/E 输入 n(1≤n≤1e5) m(1≤m≤20) 和长为 n 的字符串 s,由前 m 个小写字母组成。 你需要构造一个长为 m 的小写字母排列,例如 m=3 时的 bac,把这个排列当成一个只有一排的键盘。 在只用一根手指的情况下,用这个键盘打出 s。 问:构造一个怎样的键盘,可以使手指的移动距离之和最小?输出这个最小值。
本质是要最小化 pos[x]-pox[y],其中 x,y 为 s 中相邻字符,因此要统计字符串中相邻字母对的个数,记作 cnt。
用状态 s 表示前面填了 |s| 个字母的键盘,这里 |s| 表示 s 中二进制 1 的个数
假设当前填字母 c,那么 c 的位置 pos[c]=|s|。
对于前面已经填的字母 x,贡献为 cnt[c][x] * (pos[c] - pos[x]),
对于后面没有填的字母 y,贡献为 cnt[c][y] * (pos[y] - pos[c])。
但是此时还不知道 y 的具体位置,怎么转化?只统计 c 对答案的贡献!把 cnt[c][x] * pos[c] 单独分离出来,这样每个字母怎么填,就不需要知道前后字母的【具体位置】了。
总贡献 cost(c) = sum(cnt[c][x] * pos[c] for x in s) - sum(cnt[c][y] * pos[c] for y not in s)
定义 f[s] 表示状态 s 的 cost 之和的最小值,有
f[s|c] = min(f[s] + cost(c) for c not in s)
初始值 f[0] = 0,答案为 f[-1]。
for (int i = 0; i < n - 1; i++)
{
int x = s[i] - 'a', y = s[i + 1] - 'a';
if (x != y)
cnt[x][y] ++, cnt[y][x] ++;
}
int f[1 << m];
memset(f, 0x3f, sizeof f);
f[0] = 0;
for (int s = 0; s < 1 << m; s++)
{
int one = __builtin_popcount(s);
for (int i = 0; i < m; i++)
if ((s >> i & 1) == 0)
{
// 加第 i 个字母
int sum = 0;
for (int j = 0; j < m; j++)
if (s >> j & 1) sum += cnt[i][j] * one;
else sum -= cnt[i][j] * one;
f[s | (1 << i)] = min(f[s | (1 << i)], f[s] + sum);
}
}
cout << f[(1 << m) - 1] << endl;MEX 子序列
https://codeforces.com/problemset/problem/1613/D 输入 T(≤1e5) 表示 T 组数据。所有数据的 n 之和 ≤5e5。 每组数据输入 n(1≤n≤5e5) 和长为 n 的数组 a(0≤a[i]≤n)。 称序列 b 为 MEX 序列,如果对所有 i 都有 abs(b[i] - mex(b[0],...,b[i])) ≤ 1 成立,其中 mex(S) 表示不在 S 中的最小非负整数。 输出 a 的非空 MEX 子序列的个数,模 998244353。 两个子序列只要有元素下标不同,就算不同的子序列。例如 a=[0,0,0] 有 7 个不同的非空子序列。 注:子序列不要求连续。
MEX 序列只能有两种形式:
- [0,...,0, 1,...,1, ..., x-1,...,x-1, x,...,x]
- [0,...,0, 1,...,1, ..., x-1,...,x-1, x+1,...,x+1, x-1,...,x-1, x+1,...]
设 dp1(i,j) 表示考虑前 i 个数,mex=j 的第一种 mex 序列个数,dp2(i,j) 表示第二种
当前是 dp1(i,j),考虑 x 怎么更新答案(当前是 dp2(i,j))
- 若 x<j-1,不能更新 (不能更新)
- 若 x=j-1,不改变 mex 的值,可转移到 dp1(i+1,j) (不改变,转移到 dp2(i+1,j))
- 若 x=j,mex 的值会 +1,可转移到 dp1(i+1,j+1) (mex 的值会 +2,不能更新)
- 若 x=j+1,mex 的值不变,但是转移到 dp2(i+1,j) (不改变,转移到 dp2(i+1,j))
- 若 x>j+1,不能更新 不能更新
代码实现时可优化第一个维度,原地更新
vector<LL> f1(n + 2), f2(n + 2);
f1[0] = 1;
while (n -- )
{
cin >> x;
f1[x + 1] = (f1[x + 1] + f1[x + 1]) % mod;
f1[x + 1] = (f1[x + 1] + f1[x]) % mod;
if (x > 0) f2[x - 1] = (f2[x - 1] + f2[x - 1]) % mod;
if (x > 0) f2[x - 1] = (f2[x - 1] + f1[x - 1]) % mod;
f2[x + 1] = (f2[x + 1] + f2[x + 1]) % mod;
}
LL res = 0;
for (int x: f1) res = (res + x) % mod;
for (int x: f2) res = (res + x) % mod;
cout << (res - 1) % mod << endl; // 非空 -1字符矩阵中的回文路径数
https://codeforces.com/problemset/problem/570/E 输入 n m (1≤n,m≤500) 和 n 行 m 列的字符矩阵,只包含小写字母。 你需要从左上角的 (1,1) 出发,到达右下角的 (n,m)。 每次只能向下或向右走。 问:有多少条路径对应的字符串是回文串?(见右图) 模 1e9+7。
转换成两个人同时从左上和右下出发,定义 f[i][r1][r2] 表示走了 i 步,两人分别在第 r1 行和第 r2 行的方案数。这样只需要三个数就能表示坐标 (r1,c1) 和 (r2,c2)。
f[0][1][n] = 1(如果 a[1][1] != a[n][m] 直接输出 0)
如果 a[r1][c1] = a[r2][c2],那么 f[i][r1][r2] = f[i-1][r1][r2] + f[i-1][r1][r2+1] + f[i-1][r1-1][r2] + f[i-1][r1-1][r2+1],否则就是 0
代码实现时,第一个维度可以去掉。
最后答案按照字符串长度的奇偶性讨论。
如果是奇回文串,那么答案为 sum(f[i][i]),否则答案为 sum(f[i][i]+f[i][i+1])。
LL f[n + 1][n + 2];
memset(f, 0, sizeof f);
f[1][n] = 1;
for (int i = 1; i < (n + m) / 2; i++) // 路径长度 n+m-1 步数除以2 上取整
for (int r1 = n; r1 > 0; r1--)
for (int r2 = 1; r2 <= n; r2++) {
int c1 = i + 2 - r1, c2 = m + n - i - r2;
if (c1 > 0 && c1 <= m && c2 > 0 && c2 <= m) {
if (a[r1 - 1][c1 - 1] == a[r2 - 1][c2 - 1])
f[r1][r2] = (f[r1][r2] + f[r1 - 1][r2] + f[r1][r2 + 1] + f[r1 - 1][r2 + 1]) % MOD;
else f[r1][r2] = 0;
}
}
LL res = 0;
if ((n + m) % 2) {
for (int i = 1; i <= n; i++)
res = (res + f[i][i] + f[i][i + 1]) % MOD;
} else {
for (int i = 1; i <= n; i++)
res = (res + f[i][i]) % MOD;
}数位 DP + 预处理
https://codeforces.com/problemset/problem/55/D
输入 T(≤10) 表示 T 组数据。 每组数据输入 L R(1≤L≤R≤9e18)。
输出 [L,R] 内有多少个数字,能被其每个非零数位整除? 例如 240 能被 2 和 4 整除,符合要求。
如果一个数字 num 被多个数整除,那么 num 也被这些数的最小公倍数(LCM)整除。
比如 num 被 6,4,3 整除,那么 num 也必然被 12 整除。
考虑到 LCM(1,2,3,...,9) = 2520,我们无需在记忆化搜索时记录 num,而是记录 num % 2520。
如果 num % 2520 能被 num 的所有非零数位的 LCM 整除,那么 num 也同样能被 LCM 整除。
定义 dfs(i,j,rem) 表示当前枚举到第 i 个数位,之前枚举的数位的 LCM 为 j,num % 2520 = rem。
递归终点:如果 i = n 时 rem % j = 0,则说明构造的 num 是合法的,返回 1,否则返回 0。
由于 j 最大是 2520,直接创建 925202520 的 64 位整形数组是会 MLE 的(约 436MB)。
可以预处理 {1,2,3,..,9} 的所有非空子集的 LCM(这有 48 个),把这 48 个数离散化一下,就可以大大减少空间了。
另外在 dfs 中算 LCM 可能有点慢,可以打表预处理这 48 个数与 1~9 的 LCM 的结果。
int lcms[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12,
14, 15, 18, 20, 21, 24, 28, 30, 35, 36, 40,
42, 45, 56, 60, 63, 70, 72, 84, 90, 105, 120,
126, 140, 168, 180, 210, 252, 280, 315, 360, 420, 504, 630, 840, 1260, 2520};
int idx[2521], lcmRes[48][10];
void init() {
for (int i = 0; i < 48; i++) idx[lcms[i]] = i;
for (int i = 0; i < 48; i++) {
int v = lcms[i];
lcmRes[i][0] = lcmRes[i][1] = i;
for (int j = 2; j < 10; j++) lcmRes[i][j] = idx[(int)lcm(v, j)];
}
}
LL dfs(int i, int j, int rem, bool limitLow, bool limitHigh) {
if (i == n) return rem % lcms[j] ? 0LL : 1LL;
if (!limitLow && !limitHigh && f[i][j][rem] != -1) return f[i][j][rem];
int lo = limitLow ? low[i] - '0' : 0;
int hi = limitHigh ? high[i] - '0' : 9;
LL res = 0;
for (int d = lo; d <= hi; d++)
res += dfs(i + 1, lcmRes[j][d], (rem * 10 + d) % 2520, limitLow && d == lo, limitHigh && d == hi);
if (!limitLow && !limitHigh) f[i][j][rem] = res;
return res;
}括号:最长合法子串个数
https://codeforces.com/problemset/problem/5/C 给出一个括号序列,求出最长合法子串和它的数量。 合法的定义:这个序列中左右括号匹配
用栈模拟,如果可以匹配则把值置为 1,然后求最长的连续 1 的个数即可
/*
**()()))())()()(()**
**1111001101111011**
*/
vector<bool> st(n + 1);
stack<int> s;
for (int i = 0; i < n; i++)
if (str[i] == '(') s.push(i);
else if (s.size()) {
st[s.top()] = st[i] = 1;
s.pop();
}
int mx = 0, cnt = 0;
for (int i = 0; i <= n; i++)
if (st[i]) cnt ++;
else mx = max(mx, cnt), cnt = 0;
int tot = 0;
for (int i = 0; i <= n; i++)
if (st[i]) cnt ++;
else {
if (cnt == mx) tot ++;
cnt = 0;
}子序列乘积为完全平方数
https://codeforces.com/problemset/problem/895/C
输入 n(1≤n≤1e5) 和长为 n 的数组 a(1≤a[i]≤70)。 输出有多少个非空子序列,其元素乘积是完全平方数。模 1e9+7。
统计每个元素的出现次数,记到 cnt 数组中。
70 以内有 19 个质数,考虑状压 DP。
定义 f[x][s] 表示考虑从 1 到 x 中选择子序列的方案数,满足子序列乘积的质因子分解中出现奇数次的质因子的集合是 s。
设 x 出现了 c=cnt[x] 次。
如果选择偶数个 x(这样的方案有 pow(2,c-1) 个),那么 s 不变,有
f[x][s] += f[x-1][s] * pow(2,c-1)
如果选择奇数个 x(这样的方案有 pow(2,c-1) 个),那么 s 变成 s XOR mask,其中 mask 是 x 的质因子分解中出现奇数次的质因子的集合,有
f[x][s XOR mask] += f[x-1][s] * pow(2,c-1)
注:转移方程是用刷表法思考的。
初始值 f[0][0] = 1。
答案为 f[70][0]。
代码实现时,可以用滚动数组优化空间。
vector<LL> f(1 << primes.size());
f[0] = 1;
for (int i = 1; i <= 70; i++) {
int x = i, c = cnt[i];
if (c == 0) continue;
int mask = 0;
for (int j = 0; j < primes.size(); j++)
for (; x % primes[j] == 0; x /= primes[j])
mask ^= 1 << j;
vector<LL> g(f.size());
for (int j = 0; j < f.size(); j++) {
g[j] = (g[j] + f[j] * pow2[c - 1]) % MOD;
g[j ^ mask] = (g[j ^ mask] + f[j] * pow2[c - 1]) % MOD;
}
f = std::move(g);
}
cout << (f[0] - 1 + MOD) % MOD << endl;